什么是阻抗？

这既是社区的资源，也是我自己的学习经验。我对这个主题只有足够的了解，可能会惹上麻烦，但是我对这个主题的细节没有最好的了解。一些有用的响应可能是：

• 阻抗成分说明
• 这些组件如何相互作用
• 一个如何转换阻抗
• 这与RF滤波器，电源以及其他任何东西有什么关系...

谢谢您的帮助！

对于“什么是阻抗”这个问题，我要指出的是，阻抗通常是物理学的一个广义概念，电阻抗只是一个例子。

为了了解其含义及其工作原理，通常更容易考虑机械阻抗。考虑尝试将沉重的沙发推（滑）过地板。
您施加一定的力，然后沙发以一定的速度滑动，具体取决于您用力的程度，沙发的重量，地板的类型，沙发的支脚的类型等等。在这种情况下，可以定义一个机械阻抗，该机械阻抗给出了推压力度和卧推速度之间的比率。

实际上，这很像直流电路，在电路上施加一定量的电压，电流以一定的相应速率流过该电路。

对于沙发和电路而言，对输入的响应可能是简单且相当线性的：一个遵循欧姆定律的电阻，其电阻抗仅是电阻，沙发上可能有摩擦滑块脚，因此以与您的力量成比例的速度运动。*

电路和机械系统也可能是非线性的。如果电路由跨接在电阻上的可变电压组成，该电阻与二极管串联，则电流将接近零，直到超过二极管的正向电压为止，根据欧姆定律，此时电流将开始流经电阻。法。同样，坐在地板上的沙发通常会产生一定程度的静摩擦：只有在您施加一定程度的初始力后，沙发才会开始移动。在机械系统和电气系统中，都无法定义单个线性阻抗。相反，您能做的最好的就是分别定义不同条件下的阻抗。（现实世界更像这样。）

即使情况非常清楚和线性，也必须注意，阻抗仅描述了一个比率，它并没有描述系统的极限，也并不“不好”。通过增加更多的电压/加大推力，您绝对可以在理想的系统中获得所需的电流/速度。

机械系统也可以为交流阻抗提供很好的感觉。想象一下您正在骑自行车。每踩半个踏板，您就向左推，向右推。您还可以想象只用一只脚和脚趾夹踩踏板，这样您就可以在踏板的每个循环中进行推拉。这很像向电路施加交流电压：您以某个给定的频率周期性地推拉。

如果频率足够慢-例如当您停在自行车上时，踩下踏板的问题就只是一个“直流”问题，例如推沙发。但是，当您加快速度时，事情可能会有所不同。

现在，假设您以一定速度骑车，而您的自行车是三速，低，中和高传动比。中等的感觉很自然，齿轮很难施加足够的力来产生任何变化，而在低速档时，您只需旋转踏板就不会将任何能量传递到车轮上。这是阻抗匹配的问题，在这种情况下，只有当车轮对您的脚产生一定程度的物理阻力时，您才能有效地将动力传递给车轮。相应的电气现象也很常见。您需要阻抗匹配的线才能有效地将射频功率从A点传输到B点，并且每当将两条传输线连接在一起时，接口上都会有些损耗。

踏板对脚的阻力与踩踏的力度成正比，这与简单的阻力（尤其是低速行驶）最密切相关。即使在交流电路中，电阻器的行为也类似于电阻器（达到特定点）。

但是，与电阻不同，自行车的阻抗取决于频率。假设您从停车处开始将自行车置于高档。入门可能非常困难。但是，一旦开始使用，踏板所表现出的阻抗就会随着您走得更快而降低，而一旦您走得很快，您可能会发现踏板所表现出的阻抗太小而无法吸收脚的力量。因此，实际上存在一个随频率变化的阻抗（电抗），该阻抗开始时较高，而随着您移向较高的频率，阻抗会降低。

这很像电容器的行为，自行车的机械阻抗的一个很好的模型是电阻与电容器并联。

在直流电（零速度）下，您只看到高恒定电阻作为阻抗。随着踩踏频率的增加，电容器的阻抗变得低于电阻器的阻抗，并允许电流以这种方式流动。

当然，还有其他各种电气组件及其机械类比**，但是当您了解有时看起来似乎是什么的数学方面时，本讨论应该为您提供一些基本概念，使他们初步了解接地（双关语意）就像一个非常抽象的主题。

*挑剔的一句话：欧姆定律对实际设备永远都不是精确的，而现实世界中的摩擦力永远不会使速度与力成正比。但是，“相当线性”很容易。我正在尝试所有教育和东西。放过我吧。

**例如，电感器就像是车轮上的弹簧滚轮，随着频率增加，它会增加阻力。

电路元件的阻抗是该元件中电压与电流之比。

恒定电压和电流

对于恒定的电压和电流，阻抗就是电阻。电阻器是一种即使电压变化也能保持相同的电压电流比的设备。它们是线性的-电压加倍，电流也加倍。如果绘制电压与电流的关系图，则斜率就是阻抗。

就像两个金属板一样的电容器，对于恒定的电流和电压，就像开路一样。电感器，意味着卷曲的电线，对于恒定电流和电压而言就像短路一样。

（实际上，这还不是很干净。电阻趋于热态时，它们会允许流过的电流比应该流过的少。电容器会泄漏一点点电流，即使它们本来也不会通过。电感器的电阻很小，像任何普通的电线一样。）

电压和电流随时间变化

这就是它变得更有趣的地方。某些电路元件（例如电容器和电感器）根据所承受电压的频率允许或多或少的电流流动。您可以将它们视为与频率相关的电阻器。阻抗的频率相关部分称为电抗。添加电抗和电阻，即可获得阻抗。

电抗的例子

假设您有一个产生振幅为120 V的正弦波的盒子。您将该盒子设置为每秒60个周期，并将该盒子的信号连接到一个0.1 F的电容器上。流过的电流将是相同频率的正弦波。当前将是：

I = V * 2 * pi *频率* C

I = 120 * 2 * 3.14 * 60 * 0.1 = 4522安培

（实际上，这么大的电流会使电容器爆炸。）

如果将正弦波的频率加倍，则电流将加倍。这种行为在RC滤波器中很有用-例如，您可以使电路在一个频率下具有高电阻，而在另一频率下具有低电阻，这使您可以从噪声中挑选出信号。

电感的行为类似，但是随着频率的增加，阻抗会增加而不是减少。

现实世界

实际上，所有东西都具有一定的电阻和电抗（只有一点电容或电感，但不能两者都有）。此外，所有电路都具有非线性，例如温度依赖性或几何效应，使它们偏离理想模型。

此外，我们处理的电压和电流绝不是完美的正弦波-它们是频率的混合。

例如，假设您正在运行螺线管来打开门锁，例如公寓楼中的蜂鸣器。螺线管是一个巨大的感应器，它产生的磁场会克服弹簧力将闩锁拉回原处。当您关闭电磁阀时，电流会随着时间急剧变化。当您尝试使电流快速下降时，螺线管的电感会使电压快速上升。

这就是为什么您会看到与大型电感器并联的“反激二极管”的原因-允许电流下降得更慢，从而避免了由高频变化引起的电压尖峰。

下一步

从这里开始，下一步是学习如何对由多个电抗元件（例如一堆电阻和电容器）组成的电路建模。为此，我们不仅要跟踪电压和电流的幅度，还要跟踪它们之间的相移-正弦波的峰值没有及时对齐。

（不幸的是，我必须在这里完成一些工作，所以我必须离开这个链接：http : //www.usna.edu/MathDept/CDP/ComplexNum/Module_6/ComplexPhasors.htm）

阻抗是电阻概念的扩展，包括电容和电感的影响。电感器和电容器具有“电抗”，而阻抗是电阻和电抗效应的组合。

n00b简介：从本质上讲，它使您可以将电容器和电感器当作电阻来考虑，从而使计算更简单，更直观。例如，如果您知道如何计算纯电阻分压器的输出：

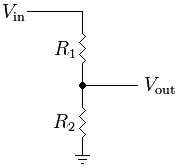
那么您还可以计算给定频率下RC滤波器的输出幅度：

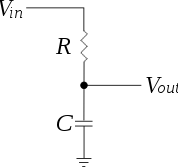
例如，假设R为1kΩ，C为1 uF，并且如果您想输入160 Hz的正弦波，则想知道输出电压。电容器在160 Hz时的电抗约为1kΩ，因此两个“电阻器”都相同，并且两端的电压也相同。每个组件上的输入电压为0.707，但在电阻情况下不是0.5。

在其他频率下，电容器电抗的大小会有所不同，这就是为什么滤波器对不同频率做出不同响应的原因。您也可以使用虚数来计算输出中的相移，但是幅度通常是您唯一关心的部分。

我喜欢阻抗的机械类比是一个垂直悬挂的弹簧，上面悬挂着重物。如果系统最初是静止的，并且对顶部的砝码进行了短暂的向上猛拉，然后迅速将其返回到其原始位置，则干扰将沿着弹簧传播。每个砝码将被上方的砝码向上拉，然后向上推至上方的砝码（并向下推），同时将其向上拉至下方的砝码（并由其向下拉），最后再由上方的砝码向上推。重量低于。一旦发生所有这些事情，配重将返回其原始位置和（零）速度。

请注意，向下传播的波的行为不依赖于其下方的任何东西。但是，一旦波到达底部，则可能会发生以下三种情况之一，具体取决于弹簧的末端是悬垂的，牢固地固定在某个物体上还是固定在可以抵抗某些阻力而移动的物体上。

如果弹簧的末端悬空了，则底部重物在向上晃动时将不会在其下方放下任何东西。这样的效果将是，重量将比其他情况更加猛烈向上猛拉，并且超过上述重量将抵消其能量。反过来，这将导致配重块在上面的配重块上向上推动，并产生一个向上移动的波动，该波动（在没有摩擦损失的情况下）的幅度将等于初始的向下波动。位移方向将与原始波相同（即向上），但应力将相反（原始波为张力波；回弹将为压缩）。

相反，如果弹簧的端部固定，则底部重量将发现其下方的弹簧的抵抗力比预期的要强。因此，底部的重量将不会像预期的那样上升，而最终的效果似乎是底部产生了额外的“拉力”，从而向上方发出了波浪。该波的位移方向将与原始波相反（即向下），但应力将相同（压缩）。

如果弹簧的底部连接到稍微移动但不如悬挂弹簧那么大的物体上，则上述两种行为可能会在某种程度上抵消。如果允许弹簧的底部移动正确的量，则行为将取消，并且波将消失。否则，一个或其他类型的波将反弹，但幅度通常将小于悬空或固定端的幅度。所需的电阻量由阻抗有效地定义，而阻抗又是砝码质量和弹簧的弹簧常数的函数。

请注意，此模型捕获了许多与阻抗相关的行为。例如，如果所有重量都超过某个点重量100g，而所有重量都低于200g，并且所有弹簧均相等，则从较轻的重量到较重的重量的过渡会导致一些波能向上反射（以某种方式类似于固定的底端），因为较重的重量不会像预期的那样移动。关键概念是，对于被推回零速度的物体，它们必须同时传递动能和动量。如果他们能够将他们的能量和动量转移到具有与推动他们相同的特征的东西，他们将接受所有的能量和动量并继续下去。否则，他们将不得不发回一些能量和/或动量。

我将答案限于电气领域。阻抗（Z）实际上就是V / I。它是如此简单。但这并不是在所有情况下都这么简单。让我们从简单列表开始并逐步完善。

如果阻抗是一个简单的集总电阻，而V是一个直流电压（频率= f = 0），则可以将Z = V / I改写为R = V / I。

如果阻抗是由电容或电感引起的，则阻抗取决于频率。

如果频率足够高，以致组件不会显示为集总元件，则阻抗不仅取决于频率，而且取决于位置。有时，这些元素设计为可分布的（例如，自由空间中的波导，天线和EM波），有时则不是。

为描绘时间和空间（1维）中这些较高频率效应而开发的通用工具为。。。Z ＝ V / I。但是'V'和'I'都是（A）（e）^（j（wt + x））形式的复数向量，其中j = SQRT（-1），'A'是常数，'e '是自然对数的底数，'w'是以弧度/秒为单位的频率，'t'是以秒为单位的时间，并且'x'是沿一维路径的距离。因为“ Z”是这两个复矢量的比率，所以它也是随时间和空间变化的复矢量。电气工程师在所需的时间和位置上操纵这些量，然后取V或I（或Z）的实数部分来获得在现实世界中观察到的结果。