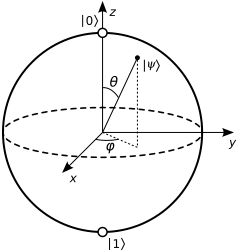
如何考虑Bloch球面中的Z门？

10

我对如何理解Bloch球面中的门感到困惑。 $Z$

考虑矩阵，可以理解的是和。 $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

在此说明， gate是绕轴旋转的旋转。然后，我应该如何理解？由于是南极，所以我自然而然地认为绕轴旋转并没有任何作用。 $Z$ $\pi$ $Z$ $Z|1\rangle = -|1\rangle$ $|1\rangle$ $\pi$ $Z$

quantum-gate bloch-sphere

— 比克
source

7

思考布洛赫球的方法是根据状态的密度矩阵。作用于或什么也不做，对于任何对角线密度矩阵都是如此。要查看旋转的效果，需要查看如何改变任何非对角密度矩阵，例如。 $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

— 达夫·沃利
source

7

$|1\rangle$ 和被分配给Bloch球面上的同一点，因为它们在全局相位上相等。代数：其中表示“等于全局相位”。意味着有一些使得。 $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

令您感到困惑的是，尽管事实是和，但对于两者的线性组合却并非如此。例如，即使。 $|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

— 克雷格·吉德尼
source

2

根据维基百科，我们可以将任何纯状态写为

| ψ ⟩ = \cos （ \frac{θ}{2} ） | 0 ⟩ + Ë^{一世 ϕ} 罪 （ \frac{θ}{2} ） | 1个 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

其中和是布洛赫球上的角度： $\theta$ $\phi$

除极点外，几乎所有点（即纯态）在角度方面都具有唯一的表示形式。就像地球上的南极没有明确定义的经度（任何经度的工作原理一样），对于状态，任何相位表示同一件事。“纬度”在这里，让我们将其插入方程式： $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1个 ⟩ = \cos （ \frac{π}{2} ） | 0 ⟩ + Ë^{一世 ϕ} 罪 （ \frac{π}{2} ） | 1个 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + Ë^{一世 ϕ} | 1个 ⟩

$= 0 + e^{i \phi} |1 \rangle$

如果您熟悉欧拉的身份，您可能会认识到是复平面中的旋转。特别地，由于是的旋转，因此得到著名的，最终得出。 $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

— 诺里乌斯
source

1

错了编写会产生误导：这些是等效状态，因为它们仅在全局相位上有所不同，但这并不意味着状态向量是相同的。之所以得到该结果，是因为您假设状态向量与Bloch球面上的点之间存在双射，而事实并非如此。双射站在布洛赫（Bloch）球面上的点之间，并且被描述为密度矩阵的状态

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

— glS

@glS谢谢，从中得出的看上去确实有些可疑。从您的角度来看，改善答案是否有意义，还是无可避免地错误？

1 = - 1

$1=-1$

— Norrius

那就是您的电话=）。我认为正确的答案是DaftWullie给出的答案（我认为提问者与您的答案中的误解相似）。对于这个问题，我没有什么可说的了

— glS