在关于文本分类的自动编码器的论文中, Hinton和Salakhutdinov演示了二维LSA(与PCA密切相关)产生的图: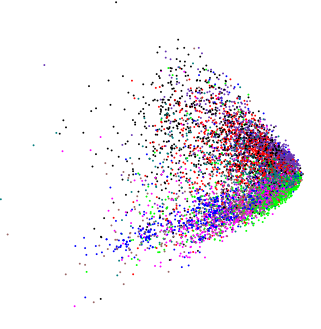 。
。
将PCA应用于绝对不同的略高维度的数据,我得到了一个看起来类似的图:( 在这种情况下,我真的很想知道是否有任何内部结构)。
在这种情况下,我真的很想知道是否有任何内部结构)。
如果我们将随机数据输入到PCA中,则会得到一个圆盘状的斑点,因此这种楔形的形状不是随机的。它本身意味着什么吗?
在关于文本分类的自动编码器的论文中, Hinton和Salakhutdinov演示了二维LSA(与PCA密切相关)产生的图: 。
。
将PCA应用于绝对不同的略高维度的数据,我得到了一个看起来类似的图:( 在这种情况下,我真的很想知道是否有任何内部结构)。
在这种情况下,我真的很想知道是否有任何内部结构)。
如果我们将随机数据输入到PCA中,则会得到一个圆盘状的斑点,因此这种楔形的形状不是随机的。它本身意味着什么吗?
Answers:
假设变量是正值或非负值,则边缘的边缘只是数据将分别变为0或负值的点。由于此类现实数据倾向于右偏,因此我们看到在其分布的低端具有更高的点密度,因此在楔形的“点”处具有更高的密度。
更一般而言,PCA只是数据的轮换,对这些数据的约束通常会以与问题所示相同的方式在主要组件中可见。
这是使用几个对数正态分布的变量的示例:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")
根据前两台PC隐含的旋转角度,您可能会看到楔形或看到一些不同的版本,在此处使用(ordirgl()代替plot())在3d中显示
在这里,在3D中我们看到多个尖峰从中心质量突出。
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")
对于统一的正随机变量,我们看到一个立方体
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")
请注意,在这里,为了说明起见,我仅使用3个随机变量显示了制服,因此这些点描述了3d中的一个立方体。具有更大的尺寸/更多的变量,我们无法在3d中完美地表示5d超立方体,因此,独特的“立方体”形状会有些失真。类似的问题会影响所示的其他示例,但是仍然很容易看到这些示例中的约束。
对于您的数据,在PCA之前对变量进行对数变换会拖尾并拉开聚集的数据,就像您可能在线性回归中使用这种变换一样。
其他形状可以在PCA图中出现。一种这样的形状是保存在PCA中的度量表示的伪像,被称为马蹄形。对于具有长梯度或主导梯度的数据(沿一维排列的样本,变量从0增大到最大值,然后沿着数据的各个部分再次减小到0,这会产生此类伪像。
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")
这会产生极端的马蹄形,轴两端的点会折回到中间。