贝叶斯定理是什么？

36

主要思想是什么，即与贝叶斯定理有关的概念？我不要求任何复杂的数学符号的派生。

probability bayesian theory

— 用户333
source

4

相关：stats.stackexchange.com/questions/22/…–

— Shane

3

我还想建议此链接为某种低级解释：yudkowsky.net/rational/bayes

— steffen 2011年

1

贝叶斯定理在没有视觉表示的情况下可能是一团糟，就像在数学中那样。为什么不对贝叶斯概率使用概率平方或概率树？当输入新数据时，它将关闭一些样本空间（例如，检测为阳性的疾病会关闭检测为阴性的样本）。然后，样本空间仅成为概率的子集（可能被测试为阳性），并且仅考虑这一点。我遇到的困难是将贝叶斯应用于概率分布而不是离散概率。数学真可怕！

22

贝叶斯定理是一个相对简单但概率论的基本结果，可以计算某些条件概率。条件概率就是那些反映一个事件对另一个事件的概率的影响的概率。

简而言之，它以最著名的形式表示，给定新数据的假设的概率（P（H | D）；称为后验概率）等于以下等式：给定假设的观测数据的概率（P（D | H）；称为条件概率），乘以理论在新证据之前为真的概率（P（H）；称为H的先验概率）除以看到该数据的概率，即周期（P（D）；称为D的边际概率。

形式上，方程看起来像这样：

$替代文字$

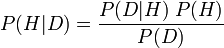
贝叶斯定理的重要性很大程度上是由于它的正确使用是概率学派之间争论的焦点。对于主观贝叶斯（将概率解释为主观信念度），贝叶斯定理通过将其主观概率判断插入等式并运行，为理论测试，理论选择和其他实践提供了基础。对于常客（将概率解释为限制相对频率），贝叶斯定理的这种使用是一种滥用，他们努力使用有意义的（非主观的）先验（在另一种概率解释下，客观的贝叶斯定理也是如此）。

— 约翰·泰勒
source

1

好答案。我有一个小疑问：使用“主观”和“客观”一词不太合适，因为没有任何方法是“客观的”。我要说的是，频繁主义者和“客观”贝叶斯主义者只是通过使用某些规则或标准来得出其概率分布。因此，常客/客观贝叶斯主义者将不再为眼前的具体情况而努力，而是会采用“默认”选择（从而隐藏其主观性）。

— 概率

如果您要测量的是实值（例如6岁儿童的身高），那么P（D）是多少？是数据的pdf吗？在这种情况下，您只需按以下方式计算后验点：

？

P (x | H | D) = \frac{P (x | D | H) P (x | H)}{P (x | D)}

$P(x|H|D) = \frac{P(x|D|H)P(x|H)}{P(x|D)}$

— naught101

13

对不起，但是这里似乎有些混乱：贝叶斯定理不适合讨论永无止境的贝叶斯- 频繁主义辩论。这是一个与两种思想流派都一致的定理（假设它与柯尔莫哥洛夫的概率公理是一致的）。

当然，贝叶斯定理是贝叶斯统计的核心，但是该定理本身是通用的。频繁主义者和贝叶斯主义者之间的冲突主要与如何定义先验分布有关。

因此，如果问题是关于贝叶斯定理（而不是贝叶斯统计）：

贝叶斯定理定义了如何计算特定的条件概率。例如，假设您知道：某人患有疾病X p（A | X）的可能性为A；某人患上疾病X p（X）的概率；一般人出现症状A p（A）的概率。利用这3条信息，您可以计算出某人患有疾病X的可能性，前提是他们患有共病A p（X | A）。

— 戴夫·凯伦
source

1

我部分不同意您的第一段，因为这些问题询问有关贝叶斯定理的概念。该频率论贝叶斯辩论是有关这个问题的这一部分。柯尔莫哥洛夫公理没有像“概率论和扩展逻辑”公理那样给贝叶斯定理同样重要的概念。

— 概率

8

$P(A|B)$ $P(B|A)$

$P(B|A)$ $A$ $P(\mbox{dice lands six})$ $P(\mbox{dice lands six}|\mbox{dice lands even})$

您可以自己得出贝叶斯定理，如下所示。从条件概率的比率定义开始：

$P(B|A) = \frac{P(AB)}{P(A)}$

$P(AB)$ $A$ $B$ $P(A)$ $A$

$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$ $AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$ $P(AB)$

$P(AB) = P(A|B)P(B)$

嘿，presto：

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

至于以这种方式旋转条件概率的意义是什么，请考虑一个常见的例子，尝试根据某人的症状来推断某人患病的概率，即我们知道他们有症状-我们可以看到它-但我们不能确定他们是否患有某种疾病并必须推断出来。我将从公式开始，然后进行重新计算。

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

因此，要解决该问题，您需要知道该症状的先验概率，该疾病的先验概率（即，该症状和疾病的常见或罕见程度），以及已知某人患有某种疾病的概率。疾病（例如，通过昂贵的耗时的实验室测试）。

它可能比这复杂得多，例如，如果您有多种疾病和症状，但是想法是相同的。更一般而言，如果您具有原因（例如疾病）和效果（例如症状）之间的概率论并且需要倒推（例如，您看到一些想要的症状），贝叶斯定理通常会出现。推断潜在疾病）。

— 安迪
source

5

统计的主要思想流派有两种：常客主义和贝叶斯主义。

贝叶斯定理与后者有关，可以被看作是一种理解理论是真的概率如何受到新证据影响的方式。这称为条件概率。你可能想看看这个让对数学的句柄。

— 托尼·布雷亚（Tony Breyal）
source

4

让我给您一个非常非常直观的见解。假设您掷硬币10次，您得到8个正面和2个反面。您会想到的问题是，这种硬币是否偏向正面。

现在，如果您按照常规定义或概率论的惯常方法，您可能会说硬币没有偏见，这是一种例外。因此，您可以得出结论，首当其冲的可能性也是50％。

但是，假设您是贝叶斯人。您实际上会认为，由于您的头数非常多，因此硬币偏向正面。有一些方法可以计算出这种可能的偏差。您将计算它们，然后当您下次抛硬币时，您肯定会叫一个头。

因此，贝叶斯概率与您根据观察到的数据发展出的信念有关。我希望这很简单。

— 赫拉迪斯
source

当然，抛硬币中的数据不仅仅只是结果-明智的贝叶斯方法甚至可能会下注，因为过去的数据量很大，而且硬币和硬币的翻转看起来很公平。除非，也许您看不到硬币或硬币被翻转。在这种情况下，您甚至都不知道数据是否只是从伪造的开始就开始了，您不妨将先验信息

— 扔到

3

贝叶斯定理涉及两个概念：概率和可能性。概率说：给定这种模型，这些就是结果。所以：给定一个公平的硬币，我将有50％的时间获得正面评价。可能性说：鉴于这些结果，这就是我们可以对模型所说的。因此：如果您将硬币掷100次并获得88个头（以便在前面的示例中使用并使其更加极端），那么公平硬币模型正确的可能性就不会很高。

用于说明贝叶斯定理的标准示例之一是检验某种疾病的想法：如果您对10000人口中有1个人患有的疾病进行了95％准确的检验，并且检验呈阳性，那么机会是多少你有病吗

天真的答案是95％，但这忽略了一个问题，即在10000人中，有9999人中有5％的测试会给出误报。因此，患这种疾病的几率远远低于95％。

我故意使用模糊的短语“机会是什么”。使用概率/可能性语言：测试准确的概率为95％，但是您想知道的是患病的可能性。

稍微偏离主题：贝叶斯定理在所有教科书中都用来解决的另一个经典示例是蒙蒂·霍尔（Monty Hall）问题：您正在参加测验。三扇门之一后面有奖。您选择第一扇门。主持人打开三扇门，没有发现任何奖金。如果有机会，您是否应该换到第二扇门？

我喜欢这个问题的措辞（由下面的参考资料提供）：您正在参加问答游戏。一百万扇门背后有奖品。您选择第一扇门。主机打开除104632门外的所有其他门，以显示没有奖品。您应该换门104632吗？

我最喜欢的从贝叶斯角度讨论贝叶斯定理的书是David JC MacKay撰写的“信息理论，推理和学习算法”。这是剑桥大学出版社的一本书，ISBN-13：9780521642989。我的回答是（我希望）对本书中所进行的讨论的提炼。（适用通常的规则：我与作者没有任何隶属关系，我只喜欢这本书）。

3

最明显形式的贝叶斯定理只是对两件事的重新陈述：

联合概率在其参数是对称的 $P(HD|I)=P(DH|I)$
$P(HD|I)=P(H|I)P(D|HI)$

因此，通过使用对称性：

P (H D | I) = P (H | I) P (D | H I) = P (D | I) P (H | D I)

$P(HD|I)=P(H|I)P(D|HI)=P(D|I)P(H|DI)$

$P(D|I) \neq 0$ $P(D|I)$

P (H | D I) = P (H | I) \frac{P (D | H I)}{P (D | I)}

$P(H|DI)=P(H|I)\frac{P(D|HI)}{P(D|I)}$

就是这样吗？如此简单的事情怎么会如此出色？与大多数事情一样，“旅途比目的地重要”。贝叶斯定理之所以如此，是因为它引起了争论。

$P(H|I)=1-P(\overline{H}|I)$

现在，演绎逻辑中的“规则”是，如果您具有关系“ A表示B”，那么您也将具有“不B表示不是A”。因此，我们有“一致推理蕴含贝叶斯定理”。这意味着“非贝叶斯定理意味着不一致的推理”。即，如果您的结果在某些先验和可能性上不等于贝叶斯结果，那么您的推理就不一致。

此结果称为Cox定理，并在1940年代的“概率推断代数”中得到了证明。可能性理论给出了一个最近的推论：科学逻辑。

— 概率逻辑
source

2

我真的很喜欢凯文·墨菲（Kevin Murphy）对贝叶斯定理的介绍 http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

引用来自经济学家的文章：

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

贝叶斯方法的本质是提供一个数学规则，解释如何根据新证据改变现有的信念。换句话说，它使科学家可以将新数据与他们现有的知识或专长相结合。典型的例子是想象一个早熟的新生儿观察到他的第一个日落，并想知道太阳是否会再次升起。他为两种可能的结果分配了相等的先验概率，并通过将一个白色和一个黑色大理石放入袋子来表示这一点。第二天，当太阳升起时，孩子将另一个白色大理石放在袋子里。因此，从袋子中随机抽出大理石的可能性是白色的（即孩子对未来日出的信心程度）从一半变为三分之二。第二天日出后这个孩子又添加了一块白色大理石，其可能性（因此，信念度）从三分之二变为四分之三。等等。渐渐地，最初认为太阳每天早晨都不会升起的最初信念被修改为几乎确定太阳将永远升起。

— art
source