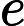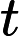在集合理论中，自然数$\mathbb{N} = \{0, 1, 2, 3, ...\}$通常被编码为纯集，即仅包含空集或其他纯集的集。但是，并非所有的纯集都代表自然数。挑战在于确定给定的纯集是否表示自然数的编码。

自然数的编码以下列方式¹起作用：

• 零是空集：$Set(0) = \{\}$
• 对于许多$n > 0$：$Set(n) = Set(n-1) \cup \{Set(n-1)\}$

因此，前几个自然数的编码是

• $0 \leadsto \{\}$
• $1 \leadsto \{0\} \leadsto \{\{\}\}$
• $2 \leadsto \{0,1\} \leadsto \{\{\},\{\{\}\}\}$
• $3 \leadsto \{0,1,2\} \leadsto \{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}$
• $4 \leadsto \{0,1,2,3\} \leadsto \{\{\},\{\{\}\},\{\{\},\{\{\}\}\},\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}\}$

任务

• 给定一个表示纯集合的字符串，请根据上述构造确定该集合是否编码自然数。
• 但是请注意，集合的元素没有排序，因此$\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}$不是唯一的有效表示$3$如例如$\{\{\{\}\},\{\},\{\{\{\}\},\{\}\}\}$表示同一组。
• 您可以使用[]，()或<>代替{}。
• 您可以假定给出的集合没有,as分隔符。
• 你可以假设不会有输入任何重复的元素，比如{{},{}}是不是一个有效输入，并且输入是良好的形成，如无{{},，{,{}}或类似的。

测试用例

真正：

{}
{{}}
{{},{{}}}
{{{}},{}}
{{},{{}},{{},{{}}}}
{{{},{{}}},{},{{}}}
{{{{}},{}},{{}},{}}
{{},{{}},{{},{{}}},{{},{{}},{{},{{}}}}}
{{{{{}},{}},{{}},{}},{{}},{},{{},{{}}}}
{{},{{}},{{},{{}},{{},{{}}},{{},{{}},{{},{{}}}}},{{{}},{}},{{},{{}},{{},{{}}}}}
{{{{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}}

假：

{{{}}}
{{{{}}}}
{{{{}},{}}}
{{},{{}},{{{}}}}
{{{},{{}}},{{}}}
{{{{{}}},{}},{{}},{}}
{{},{{}},{{},{{}}},{{},{{}},{{{}}}}}
{{{{{}},{}},{{{}}},{}},{{}},{},{{},{{}}}}
{{{{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}},{{{{{}},{}},{{}},{}},{{{}},{}},{{}}},{{{{}},{}},{{}},{}},{{{}},{}},{{}},{}}

^{相关内容：自然构造（输出给定自然数的设置编码。）
1参见https://en.wikipedia.org/wiki/Set-theoretic_definition_of_natural_numbers}

JavaScript（Node.js），53 48 44字节

f=a=>(a=eval(a)).every(e=>a[e.length]&&f(e))

在线尝试！测试用例大多是从@Arnauld的答案中被无耻地偷走的。说明：如果集合表示自然数，则它表示的自然数必须等于集合的大小，并且（如果保证保证元素是不同的），元素必须是小于自然数的表示，因此，这些长度必须较短。这当然是空的。编辑：由于@Arnauld，节省了5个字节。@Cowsquack节省了4个字节。

Python 3中，69 58 44个字节

感谢Outgolfer的Erik提供了11个字节。

多亏了Xcoder先生，才有了14个字节。

f=lambda s:all(len(e)<len(s)*f(e)for e in s)

在线尝试！

Wolfram语言（Mathematica），60 59字节

E!=(If[Sort@#===Range[t=Tr[1^#]]-1,t,E]&//@ToExpression@#)&

在线尝试！

该解决方案的核心是功能

If[Sort@#===Range[t=Tr[1^#]]-1,t,E]&

它将{0,1,2,...,n-1}以任何顺序将表单列表转换为输出n（特别是将转换{}为0），并将其他任何形式转换为实数E。

调用此函数f。给定诸如之类的输入"{{{}},{}}"，我们执行以下操作：

1. 将字符串转换为Mathematica表达式。
2. 应用于f各个级别，获得f[{f[{f[{}]}], f[{}]}]。
3. 评估所有f都会为代表它的输入产生一个自然数。例如，f[{f[{f[{}]}], f[{}]}]= f[{f[{0}], 0}]= f[{1, 0}]= 2。其他都会产生E。
4. 我们通过检查结果是否为自然数来检验结果是否为自然数E。

Brachylog（v2），9个字节

↰ᵐo.t~k|Ė

在线尝试！

通常，对于决策问题，这是一个完整的程序。输入来自标准输入，使用方括号。输出为标准输出，true.相对于false.。

说明

尽管上面我说过这是一个完整的程序，但实际上比它有趣。这是两个完整的程序和功能。当用作完整程序时，它会打印true.该集合是自然数还是false.不是自然数。当用作函数时，它“规范化”自然数（即规范化其所有元素并按值对它们进行排序；此程序在内部使用列表，而不是集合），或“引发异常”（实际上是失败，因为这是Prolog），如果输入的不是自然数。

完整程序的行为很容易解释：在B​​rachylog对不包含I / O指令的完整程序的处理中，这完全是隐含的。有问题的行为是“运行该函数，从标准输入中获取其输入，并断言其输出与第一个命令行参数给出的描述相匹配；如果断言失败或程序引发异常，则print false.，否则为print true.” 。在这种情况下，缺少命令行参数（即“一切都行”），因此该函数的异常/无异常行为给出了输出。

至于功能行为：

↰ᵐo.t~k|Ė
↰ᵐ          Map a recursive call to this function over the list
  o         Sort the list
   .   |    Assert that the following operation need not change the list:
    t         Take the last (i.e. greatest) element of the list
     ~k       Append an arbitrary element to the resulting list
   .   |    Output the unchanged list
       |    Exception handler: if the above threw an exception,
        Ė     Assert that the input is empty, and output an empty list

自然数定义为包含两个部分：自然数的以下元素，与自然数本身结合在一起。因此，其所有元素也是自然数。我们可以通过以下方法来识别自然数：a）验证其所有元素都是自然数，b）验证集合的最大元素与没有其最大元素的集合相同。

当我们使用列表而不是集合（因此使用方括号）时，我们需要将它们置于一致的顺序中，以使相等性比较有效（在这种情况下，按“值”排序）。Brachylog的默认排序顺序将在列表本身之前对列表的前缀进行排序，这方便地意味着它将对数字进行自然数排序。因此，我们可以对所有数字进行递归排序，以使它们保持一致的顺序。实际上，通过我们递归定义的函数，我们可以同时获得两个结果：对数字的元素进行递归排序，并验证它是自然数。

因此，该功能具有四个主要部分。↰ᵐ是递归调用，请确保每个元素都是自然数，然后将每个元素转换为规范化形式。o将数字本身归一化（它的元素已经被归一化，所以我们要做的就是对它进行排序）。然后，.t~k|通过检查最大元素和其他元素是否相同来确保我们具有所需的结构。空列表（即0）没有最后一个元素，因此使用会导致断言失败t。在|Ė处理这种情况下，通过在输入列表是空的情况下给出一个明确的回退。

K（ngn / k），26 24 27字节

~^{$[#(!#x)^o'x;0N;#x]}@`j@

在线尝试！

输入是解析为的json字符串`j@（特定于ngn / k的语法）

{ }是带参数的递归函数x。它返回由set表示的自然数x，0N如果不代表1 ，则返回null（）。

$[ ; ; ]如果是，则为其他。0为假，其他整数为真

!#x从0（含）的整数的长度x（不包括）

^ 没有

o'xo对的每个（'）元素进行递归（）x

# 长度

^ 一片空白？

~ 不

@充当虚拟最后一个动词，以便~与^组合{ }而不是应用到它

果冻，10字节

ẈṢ‘⁼Jȧ@ßƇƑ

在线尝试！

Japt，9个字节

Neil的JS解决方案端口。如果您对此表示赞成，请予以反对。

e@Ê>XÊ©ßX

尝试或运行所有测试用例

              :Implicit input of array U
e             :Does every element in U return true
 @            :When passed through the following function as X
  Ê           :Length of U
   >          :Greater than
    XÊ        :Length of X
      ©       :Logical AND with
       ßX     :A recursive call of the programme with X passed as the new value of U

红色，81字节

func[a][p: 1 foreach e to-block a[p: p *(pick[1 0](length? e)< length? a)* f e]p]

在线尝试！

类似于Leaky Nun的Python 3答案

果冻，8字节

߀Ṣ
ÇṖƤƑ

由于输入必须是字符串，因此此提交仅作为完整程序有效。

在线尝试！或验证所有测试用例

怎么运行的

߀Ṣ   Helper link. Argument: A (array)

߀    Recursively map the helper link over A.
  Ṣ   Sort the result.

这将产生输入的规范表示，仅由排序的数组组成。

ÇṖƤƑ  Main link. Argument: A (array)

Ç     Call the helper link to canonicalize the array.
   Ƒ  Fixed; call the link to the left and test if it returns its argument unchanged.
 ṖƤ       Pop prefix; for each non-empty prefix of the result, remove its last element.

果冻，7个字节

Ẉ<La߀Ạ

这是Leaky Nun的Python答案的一部分。

由于输入必须是字符串，因此此提交仅作为完整程序有效。

在线尝试！或验证所有测试用例

怎么运行的

Ẉ<La߀Ạ  Main link. Argument: A (array)

Ẉ        Width; compute the length of A's elements.
  L      Yield the length of A.
 <       Compare them, yielding an array of Booleans.
    ߀   Recursively map the main link over A.
   a     Take the logical AND of the Booleans and the results of the map.
      Ạ  All; yield 1 if and only if all ANDs yielded 1.

Wolfram语言（Mathematica），52字节

If[Max[#0/@#]<(l=2Length@#),l]&@*ToExpression/*EvenQ

在线尝试！