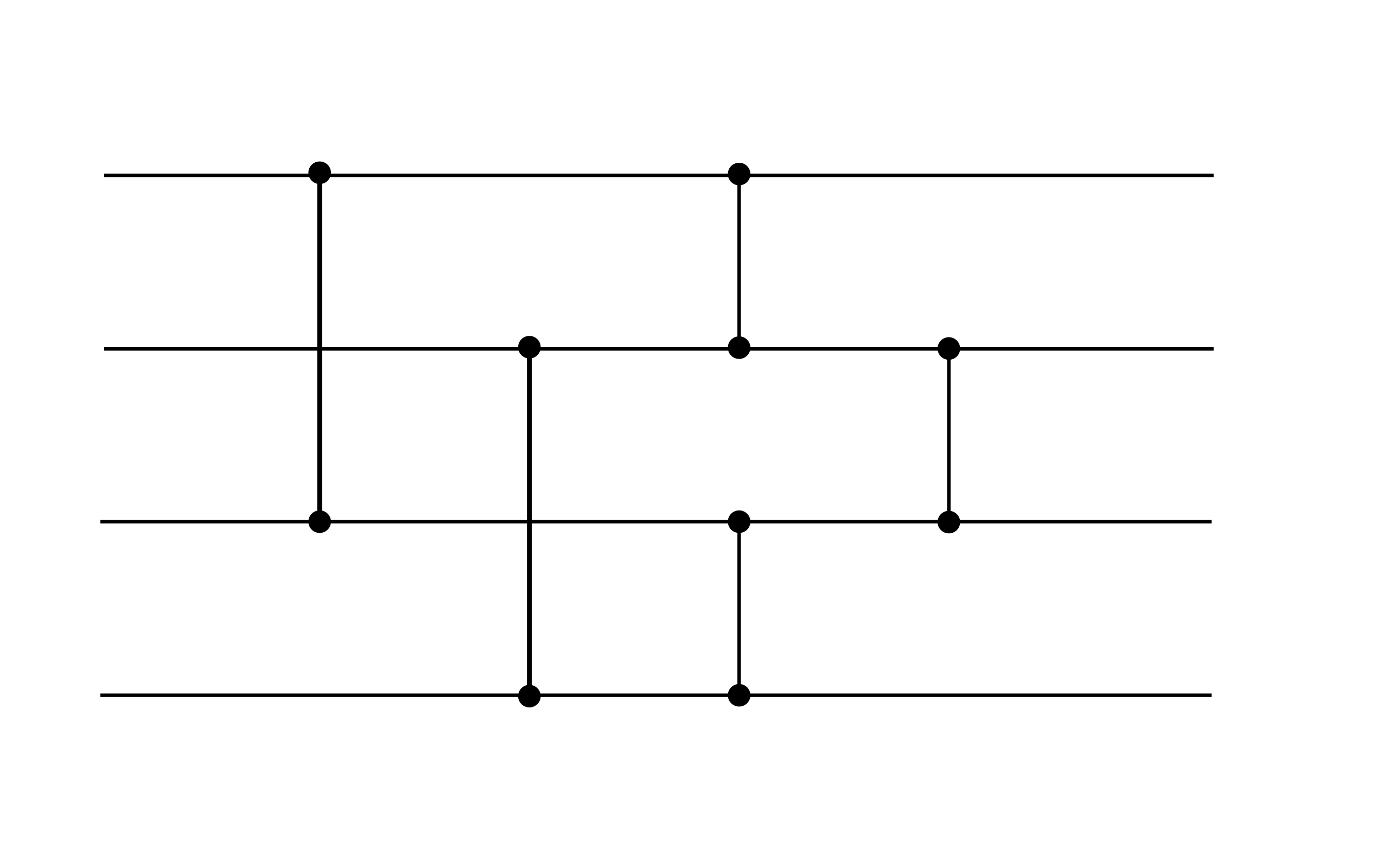
以前的神经网络高尔夫挑战（这个和那个）启发了我提出一个新的挑战：

挑战

找到最小的前馈神经网络，以便在给定具有整数条目的任何4维输入向量$(a,b,c,d)$，网络输出的坐标方向误差严格小于。$[-10,10]$$\textrm{sort}(a,b,c,d)$$0.5$

可接纳性

为了应对这一挑战，将前馈神经网络定义为层的组成。的层的功能，其由矩阵指定的权重，一个矢量的偏见，以及一个激活函数并在坐标方向上应用：$L\colon\mathbf{R}^n\to\mathbf{R}^m$$A\in\mathbf{R}^{m\times n}$$b\in\mathbf{R}^m$ $f\colon\mathbf{R}\to\mathbf{R}$

$$L(x) := f(Ax+b), \qquad x\in\mathbf{R}^n.$$

由于可以针对任何给定任务调整激活功能，因此我们需要限制激活功能的类别，以使这一挑战变得有趣。允许以下激活功能：

• 身份。 $f(t)=t$

• ReLU。 $f(t)=\operatorname{max}(t,0)$

• Softplus。 $f(t)=\ln(e^t+1)$

• 双曲正切。 $f(t)=\tanh(t)$

• 乙状结肠。 $f(t)=\frac{e^t}{e^t+1}$

总体而言，对于某个，可允许的神经网络采用的形式，其中每个层由权重，偏差和激活函数从上面的列表。例如，以下神经网络是可以接受的（虽然它不能满足此挑战的性能目标，但它可能是一个有用的工具）：$L_k\circ L_{k-1}\circ\cdots \circ L_2\circ L_1$$k$$L_i$$A_i$$b_i$$f_i$

$$\left[\begin{array}{c}\min(a,b)\\\max(a,b)\end{array}\right]=\left[\begin{array}{rrrr}1&-1&-\frac{1}{2}&-\frac{1}{2}\\1&-1&\frac{1}{2}&\frac{1}{2}\end{array}\right]\mathrm{ReLU}\left[\begin{array}{rr}\frac{1}{2}&\frac{1}{2}\\-\frac{1}{2}&-\frac{1}{2}\\1&-1\\-1&1\end{array}\right]\left[\begin{array}{c}a\\b\end{array}\right]$$

此示例显示两层。两层都具有零偏置。第一层使用ReLU激活，第二层使用身份激活。

计分

您的分数是非零权重和偏差的总数。

（例如，由于偏差向量为零，因此上面的示例得分为16。）

八度，96 88 87 84 76 54 50重量和偏差

这个6层神经网络本质上是一个3步分类网络，由一个非常简单的min/ max 网络作为组件构建而成。基本上，这是来自Wikipedia的示例网络，如下所示，但做了一些小的修改：前两个比较是并行进行的。要绕过ReLU的负数，我们只需先加100，然后再减100。

因此，由于它是幼稚的实现，因此应仅将其视为基准。但是，它会对所有大小不太大的可能数字进行完美排序。（我们可以通过将100替换为另一个数字来调整范围。）

在线尝试！

最大/最小分量

有一种（现在大大减少了优雅的方式，现在更加优雅，谢谢@xnor！）使用较少的参数来查找两个数字的最小值和最大值：

$$\begin{align} \min &= a - ReLU(a-b) \\ \max &= b + ReLU(a-b) \end{align}$$

这意味着我们必须使用更少的权重和偏见。

感谢@Joel指出，在第一步中使所有数字为正数并在最后一个数中将其取反（这将使-8权重）就足够了。感谢@xnor指出了一个更短的max / min方法，该方法使-22权重！感谢@ DustinG.Mixon提供了合并某些矩阵的技巧，这又导致了-4个权重！

function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end

在线尝试！