果冻是我们自己的丹尼斯（Dennis）提出的一种针对高尔夫的隐性编程语言。通过使用自己的代码页和强大的链接系统来简洁地表达程序，它在这里的答案越来越频繁地出现，击败了其他高尔夫类语言，例如Pyth和CJam 。

让我们收集一些在果冻打高尔夫球的有用技巧。（一如既往，请给每个答案一个提示！）

字符串压缩

如果您正在寻找一种更优化/自动的字符串压缩器，请尝试使用此压缩器。

在线尝试！

压缩的字符串看起来像“...»，其中的点是基数为250的编码数据块。解压缩算法有点复杂：该块被解释为“混合基”整数，其中会divmod分解该整数的各个部分并从中构造一个字符串。

我创建了一个小的Python 3接口来压缩Jelly字符串：

import dictionary
code_page = '''¡¢£¤¥¦©¬®µ½¿€ÆÇÐÑ×ØŒÞßæçðıȷñ÷øœþ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~¶°¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾ƁƇƊƑƓƘⱮƝƤƬƲȤɓƈɗƒɠɦƙɱɲƥʠɼʂƭʋȥẠḄḌẸḤỊḲḶṂṆỌṚṢṬỤṾẈỴẒȦḂĊḊĖḞĠḢİĿṀṄȮṖṘṠṪẆẊẎŻạḅḍẹḥịḳḷṃṇọṛṣṭụṿẉỵẓȧḃċḋėḟġḣŀṁṅȯṗṙṡṫẇẋẏż«»‘’“”'''

class Compress(list):
    def character(self, c):
        if c in '\n\x7f¶':
            o = 95
        elif ' ' <= c <= '~':
            o = ord(c)-32
        else:
            raise ValueError(c + " is neither printable ASCII nor a linefeed.")
        self += [lambda z: 3*z+0, lambda z: 96*z+o]; return self
    def string(self, s):
        for c in s: self.character(c)
        return self
    def dictionary(self, w):
        ts = bool(self)
        if w[:1] == ' ': w = w[1:]; ts = not ts
        dct = dictionary.short if len(w) < 6 else dictionary.long
        W, sc = (w, 0) if w in dct else (w[:1].swapcase() + w[1:], 1)
        if W not in dct: raise ValueError(w + " isn't in the dictionary.")
        f = ts or sc; j = (2 if sc else 1) if ts else 0; i = dct.index(W)
        self += [lambda z: 3*z+2, lambda z: 3*z+j] if f else [lambda z: 3*z+1]
        self += [lambda z: 2*z+int(len(w) < 6), lambda z: len(dct)*z+i]
        return self
    def go(self):
        compressed = []; z = 0
        for f in self[::-1]: z = f(z)
        while z:
            c = z % 250
            if c == 0: c = 250
            z = (z - c) // 250
            compressed.append(code_page[c - 1])
        return '“{0}»'.format(''.join(compressed[::-1]))

如下使用压缩机。

print(Compress()
      .dictionary('public')
      .dictionary(' static')
      .dictionary(' boolean')
      .string(' is')
      .dictionary('Power')
      .string('Of')
      .dictionary('Ten')
      .string('(')
      .dictionary('long')
      .dictionary(' input')
      .string(') {\n ')
      .dictionary(' return')
      .string('\n   ')
      .dictionary(' input')
      .string(' ==')
      .go())

Compress 是一个字符串生成器：

• .string(s) 会将原始的可打印ASCII字符插入字符串。

  （每个字符的压缩字节数约为0.827。）

• .dictionary(w)将在Jelly的内置字典中查找字符串。如果需要，可以以单个空格开头。如果这需要偏离正常的字符串添加行为，或翻转字典单词的大写字母，它将相应地添加标志。

  （短字的成本约为1.997字节，长字的成本约为2.433字节；如果有标志，请添加0.199字节。）

这是成为Jelly Wiki教程的一部分。

链条

（这是对Tacit编程的后续。）

果冻如何评估一条链？如前所述，有三种情况需要考虑：该链是被尼拉第，一元还是二元地调用的。

1.尼拉地链

这些是最简单的。要评估以尼拉德开头的尼拉德链，例如α f g h，评估该f g h尼拉德上的单链α。（注意：如果整个链为空，则返回0。如果α 不是零碎，请替换use α=0。）

例如，4½仅仅是½评估在4，这是2。

2.单子链

单子链从左到右分解，直到没有链接需要考虑为止。另外，我们在ω这里传递了一些论点。有两个问题要回答：

从左到右的评估的起始值是多少？

• 如果我们的链以nilad开头α，然后是零个或多个monad（如½），dyad-nilad对（如+2）和nilad-dyad对（如4*）：我们首先进行评估α，然后考虑链的其余部分。

• 否则，我们将从传递给该链的参数开始ω，然后考虑整个链。

我们如何沿着链条走下去？

让我们称之为V当前值-最初是上述值，但是随着我们浏览整个链，它会得到更新-并表示

• Nilads使用数字，
• 使用小写字母的单子，
• 使用运算符符号成对+，×，÷。

然后从上到下匹配以下模式：

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ω)×1 │ *
                                 │ + f ...   │ V+f(ω)  │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ω     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

让我们在链上尝试一下+²×。

• +不是骗子，所以我们从开始V = ω。
• 然后，我们将其切掉+²，匹配第二个模式，并得到V = ω+ω²。
• 然后，我们将其切掉×，匹配第五个模式，并得到V = (ω+ω²)×ω。
• 链现在是空的，(ω+ω²)×ω我们的最终结果也是空的。

3.二元链

这些基本上像单子链，但是这次有两个参数，λ（左）和ρ（右）。

起始值是多少？

• 如果该链以象的三个双字母开头+ × %，我们从开始λ+ρ，然后考虑该链× % ...。

• 否则，我们将从开始λ，并考虑整个链。

我们如何沿着链条走下去？

这次，模式是

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ρ)×1 │ *
                                 │ + × ...   │ V+(λ×ρ) │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ρ     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

让我们在链上尝试一下+×÷½。

• 链条以三个二元组开始，因此我们从开始V = λ+ρ，然后丢弃+。
• 然后，我们将其切掉×÷，匹配第二个模式，并得到V = (λ+ρ)×(λ÷ρ)。
• 然后，我们将其切掉½，匹配第六个模式，并得到V = sqrt((λ+ρ)×(λ÷ρ))。
• 链现在是空的，我们完成了。

特殊情况下的数值

这是Jelly的数字解析器的一些特殊情况：

• - 评估为 -1
• . 评估为 0.5
• ȷ计算结果为1000（ȷ是科学记数法，例如2ȷ6是2000000）
• ıevalulates到1j（ı为复数，例如2ı3是2+3j）

还值得注意的是，4ı实际上是4+1j而非4。

您可以将它们混合和匹配，例如：

• -.是-0.5和-ȷ是-1000
• -ı是-1+1j，ı-是-1j和-ı-是-1-1j
• .ȷ 是 500.0
• .ı是0.5+1j，ı.是0.5j和.ı.是0.5+0.5j
• ȷı是1000+1j，ıȷ是1000j和ȷıȷ是1000+1000j

请注意，ȷ-是0.1，但不保存任何字节以上.1。然后还有以下内容，可以通过使用内置变量10（⁵）来以相应的字节数完成操作，但是在极少数情况下内置函数不可用或省下来使用时可能有用¤：

• ȷ.是sqrt(10) ~ 3.162277，.ȷ.是sqrt(10)/2 ~ 1.5811和ȷ-.是1/sqrt(10) ~ 0.31162

优化的串式压缩机

在线尝试！

Lynn的帖子详细介绍了压缩字符串的确切含义，并提供了一个可以生成这些压缩字符串的压缩程序。然而，虽然在果冻程序摆弄周围，我发现它累有结合.dictionary并.string伴随着空间的正确展示位置等等等等，以达到最短的字符串。

因此，我决定为Lynn脚本创建一个扩展，该扩展将接受用户输入，并找到无需用户做任何工作即可压缩它的最短方法。该脚本很长，因此我添加了一个TIO链接，而不是代码本身。

程序的工作方式是使用3种不同的方法进行压缩并确定最短的方法：

1. 方法1一次只对输入的每个字节进行编码，与其他字节相比，往往会产生最长的结果。即使输入很短，它仍然设法创建相当长的选择。例如，test可以压缩的最短方法是“¡ḌY»，而此方法返回“¡⁷ƑKʂ»（长2个字节）。通常，这仅在字符串长度少于4个字符时才有效

2. 第二种方法将字符串分成单词和标点符号，因为二者以不同的方式添加到压缩器中。词典中包含的单词是使用.dictionaryLynn的代码方法添加的，与简单地通过代码点添加单词相比，该方法对它们的压缩程度更高。但是，必须按代码点添加标点符号，因为不幸的是，它们不是字典的一部分。

   标点符号包括空格，这是方法3起作用的地方，但首先要评估方法2：让我们比较压缩字符串的方法一和方法二Hello, World!（包含单词，标点符号和空格，所以很完美）。逐个字符地压缩将导致最后一个字符串“ŒCdẉa÷¹ṂȤƓ(Ẋ)»（长15个字节），事实证明，此字符串比输出Hello，World !:的简单方法更长“Hello, World!。现在让我们看一下方法二。这样就产生了压缩字符串“Ọƥ⁷Ƭė3⁶»，其重为9个字节，比旧的字符串有了很大的改进。但是，最短的Hello，World！Jelly中的程序为8个字节，因此可以改进某些地方

3. 方法3来了，它变得更短了。不出所料，Hello，World的输出当然“3ḅaė;œ»是最短的程序。那么方法3会做什么，而方法2不会做什么？方法3将孤立的空间合并为前导空间，Jelly解压缩器为其提供了标志。在压缩程序和解压缩程序的代码中，您都可以看到类似的代码if flag_space: word = ' ' + word，表明a）支持前导空格，b）节省了字节。因此，对方法二中的字符串拆分器进行了修改，以便将空格本身直接组合到字符串之后，以创建前导字符串。这意味着将Hello, World!其解析为["Hello", ",", " World", "!"]，压缩后仅6个字节（包括定界符时为8个字节）。这几乎总是最短的压缩方法，不包括我添加的“扩展名”，

这是程序的大部分内容，但是还有更多选项可以帮助它进一步压缩数据。

• 该程序通过使用Jelly使用的Dennis的sss解压缩器来检查每个压缩版本是否正确（直接进入源代码）
• 您可以通过创建第一个命令行参数来查看所有不同的压缩字符串，该参数--debug不仅显示了最短的压缩字符串，还显示了所有3个压缩字符串以及“这是最短的”副本。
• 该程序处理“非单词”

非文字

看到此消息后，我开始研究Lynn的压缩器，对其进行了破解，并对我找不到最短的压缩方式（记录为29或32字节）感到沮丧。但是，在测试我的改进时，我发现knownsJelly词典中没有这样的词。因此，我着手寻找一种方法，以尽可能短的Jelly代码压缩这些“非单词”。

我创建了一个函数（trim），该函数将字符串拆分为一个点，其中字符串的至少一部分是单词。例如，knowns将其拆分成["known", "s"]一个程序，并使其通过字典add（.dictionary）添加第一个单词，并通过.string调用添加该单词的第二部分。但这仍然留下两个边缘情况：其中没有单词的字符串（例如ajdl）和末尾带有单词的非单词（例如）abctest，它们不会被trim函数分割。

由于无法在没有单词的字符串中找到单词，因此处理这些单词的最简单，最短的方法是通过.string调用逐个字符地添加它们。因此ajdl将由添加.string('ajdl')。尽管非话，其一端与认可的话，基本上实现了微调，但在倒车时，和应用.dictionary以及.string其他方式轮前锋微调。

事实证明，从字符串的开头或结尾开始修剪字符串当然比向压缩器中添加每个字符要短，如的输入所示abctest this string，它会产生调试输出为

Original        : abctest this string

Optimised       : “¡J+v(p⁸ụƘ$,»
Seperate spaces : “Ç⁴ṭḍµḄ7oeṂdḷp»
No trimmer      : “¤ɦ?Ɓ¢#fḲOạ⁾¶ɼȥƬ»
All characters  : “µẓþ"Y7_ḣṗḢ))9Þ⁴⁺Ẉ²)ɱ»
Non-compressed  : “abctest this string
Shortest        : “¡J+v(p⁸ụƘ$,»
=====

最佳输出（使用微调器）和非最佳输出之间的差异是高达4字节（对于果冻而言）。最后，在某些情况下，字符串本身比现在考虑在内的任何压缩版本都短。

当然，这要归功于Lynn创建原始压缩器

您可以使用上标三到九（³⁴⁵⁶⁷⁸⁹）来表示一些常用的值，但这取决于命令行参数的数量，对于链接，取决于链接的参数。

• ³ 返回100，并且仅在没有输入的情况下有效。
• ⁴ 返回16，并且仅在最多有一个输入的情况下有效。
• ⁵ 返回10，并且仅在最多有两个输入的情况下有效。
• ⁶ 如果最多三个输入，则返回一个空格。
• ⁷ 如果最多有四个输入，则返回一个新行。

但是，如果有五个输入，那么您就不走运了。

最近，该语言的新版本将其值降低³到100，并引入了一些新的原子，这些原子返回值或（用于链接）它们的参数。

• ⁸ 在除传递了左参数的链接之外的所有地方返回空白列表。
• ⁹ 除了链接已传递正确参数的链接外，其他所有地方均返回256。

如果您在链接中，并且两端都有参数传递给它，那么您就不走运了。

滥用字符串错误

要感谢Adnan充分利用在编写程序来使字符串弹性化方面的这一优势。

Jelly应该有一天会进行字符算术运算，但是在那之前，我们可以利用Python会重载大多数算术运算符并且Jelly不会进行类型检查这一事实。

例如

“abcd”Ḥ

现在不应该做任何有用的事情，但是由于Ḥ（unhalve）被实现为

lambda z: z * 2

并且算术原子在深度0处矢量化（即，它们对数字或字符进行操作），上述果冻代码产生

['aa', 'bb', 'cc', 'dd']

请注意，这会产生实际的Python字符串（不应提供Jelly类型的字符串），因此这并非在所有情况下都可用。

同样，+/在连接具有相同警告的字符串时很有用。

最佳串式压缩机

最近，我问 埃里克Outgolfer添加优化串压缩机到JHT引用页面，但他们说的是

抱歉，但是压缩器似乎尚未完全实现，
它表示的压缩“ugtestslug”时间最短ugtestslug，同时“#ṀȮụḄPƇ»也可以完成工作

因此，我决定实施最佳的字符串压缩器。

简单的方法，但保证找到最小的可能值（并因此找到字节数）

从输入到stdin输出stdout。就像当初的压缩机，¶或 （面值换行符），可以输入为换行符。

尝试使用许多标点符号（例如input ¶-----¶）运行它会输出未压缩的字符串。

当然，这要归功于Lynn创造了原始的压缩机。

这是成为Jelly Wiki教程的一部分。

隐式编程

果冻是一种默认的编程语言。这意味着您可以通过将现有链接组成一个链来定义链接（功能），而无需明确地谈论所涉及的参数。通过链接的排列方式来定义参数在此组合中“流动”的方式。稍后将给出一个示例，但首先我们需要介绍一些概念。

链接的精巧是一个非常关键的概念。所有原子 -内置对象（例如+和½-）都具有固定的Ar。链接根据其适用性分为三类：

• Nilads不接受任何争论（arar 0）；除了某些I / O和有状态命令外，它们大多表示恒定值。例如，文字3是一个尼拉德。

• Monads有一个论点（arar 1）。（这里与函数式编程 monad 没有关系。）例如，½（平方根）是monad。

• 二元组有两个参数（arar 2）：一个左参数和一个右参数。例如，+是一个二元组。

（使用形容词，我们说链接是尼拉第，单子或二进）。

那么我们在编写程序时定义的链接的含义是什么？默认情况下，它们是可变参数 –也就是说，由调用方决定要使用多少个参数，对于主链接，则取决于程序要传递多少个参数。

例如，+½是+（加法）和½（平方根）的链。由于该链的各个元素分别为2和1，因此我们将其称为2，1-链。解释器具有基于链的分解规则的特定规则：这些规则指示在给定输入的情况下n，此新链接进行计算n + sqrt(n)。（您可以将其读+½为“ ...加上其平方根。”）

因此，果冻编程本质上是一种很好地学习这些规则并构成巧妙地链条以默认完成工作的艺术。

这是成为Jelly Wiki教程的一部分。

程序结构

Jelly程序中的每一行都是一个链接定义。链接基本上是功能。最底行代表“ main”：这是使用命令行中传递的参数进行评估的链接。

因此，除了最后一个链接以外的所有链接都是函数定义：您可以使用actor引用它们。例如，“ ç是该链接上方的链接，作为二元运算符（dyad）”。考虑以下示例程序，该程序计算其参数之和的平方：

+
ç²

这有点像伪代码：

define f:
    the built-in link +
define main:
    apply the dyad f
    square the result

这是成为Jelly Wiki教程的一部分。

多链链接

还记得我写过通过链接其他链接来定义链接吗？我并没有说明全部事实：实际上，这是一个两层过程。链接是链的链，默认情况下，外链仅具有单位长度。

考虑以下程序：

C+H

这是补数加上一半。它需要一个输入值n并进行计算(1-n)+(n/2)。我知道不太激动。但是结构实际上是这样的：

我们编写的链接本身实际上是一个包含单个链的链。

假设我们要计算(1-n)+(1-n)(n/2)。二元链+×将起作用：根据链规则，它会计算λ+(λ×ρ)，看起来很像我们需要的东西。但是，在我们的程序中简单地用+by 替换+×将不会：C+×H是1,2,2,1-链– 补码，然后加（参数），然后乘以一半 –计算((1-n)+n)×(n/2)。

我们希望果冻对待+×作为一个单元，使子链的1,2,1链C，+×和H。多链链接让我们做到了！要构造它们，我们使用链分隔符 øµð：在上图中，它们将引入一个新的蓝色矩形，分别为0、1和2。在我们的案例中，我们可以通过编写Cð+×µH以下内容将链条按所需方式分组：

没有办法进一步嵌套这些东西。您必须定义多个链接。

如果是TMTOWTDI，请选择适合您的连锁店。

隐性语言的优点之一是您通常无需使用变量引用就可以逃脱。但是，仅当链中的链接具有正确的联系时，此方法才有效。

例如，获取2D数组中所有数组之和的直接方法是

S€

它将和原子映射到数组的所有元素上。

现在说您有一个由原子组成的单链

*

将2D数组的每个x映射到x ^x。例如，对于A = [[1，2]，[3，1]，[2，3]]，调用链将产生[[1，4]，[27，1]，[4，27]]。

现在，我们要取每对的总和。不幸，

*S€

之所以无效，是因为*它不再像钩子一样工作（使用A本身作为正确的参数），而是作为fork，这意味着首先S€应用到A，结果是的正确参数*。

解决这个问题很容易：

*¹S€
*⁸S€

两者都产生期望的结果：*¹是一个fork，其中where ¹是标识函数，并且*⁸是atop，其中⁸是对链的左参数（A）的引用。

但是，有一种保存字节的方法！atop ḅ1（从一元转换为整数）还计算A ^A中每个数组的总和，但与不同S€，ḅ它是二元链接。

连锁，链条

*ḅ1

返回[5，28，31]（根据需要）；因为ḅ是二进位的，所以用*钩子代替分叉

整数压缩

字符串压缩在生成英语文本时很有用，但是如果您需要压缩其他类型的数据，则效率很低。因此，大多数时候您想在程序中存储一个大的固定常数，最好将其存储为整数。

现在，Jelly有自己的代码页作为常量，整数压缩算法最简单地表示在Jelly本身：

ḃ250ịØJ”“;;”’ṄV

在线尝试！

（上面的程序还包含检查以显示整数解压缩的值。）

除了仅使用整数作为整数外，还可以通过对它进行基础转换，然后将其索引为字母字母，来使用它来创建字符串。的ṃ原子自动执行此过程，并且是相当有用的，因为它可以在一个单一的字节描述解压缩的全过程（除其他字母被减压成）。

使用外部乘积创建有用的整数矩阵

这是我为这篇文章创建的要点，HTML表格式略好一些。

外部乘积quick þ可以附加到dyad上，并使dyad对其左和右参数中的每对元素起作用。它是的简写€Ð€。例如，如果我们有代码，[1,2]+€Ð€[0,10]我们可以将其缩短为[1,2]+þ[0,10] 它们都将产生[[1,2],[11,12]]。我将þ应用（例如+þ）的二元组称为外部产品二元组。

当整数是外部乘积二元组的自变量之一时，Jelly首先获取该数字的范围，然后将结果用作自变量。知道这一点，上述示例可以进一步简化为2+þ[0,10]。对于外部乘积二元组的左右参数都适用。

当单数作用于整数时，某些外部乘积二元会生成某些整数矩阵，这些矩阵可以在打高尔夫球时使用（特别是ASCII艺术挑战），但否则需要很多字节来构造。例如，=þ当应用于整数时，将n生成一个n×n单位矩阵。在线尝试=þ！

下面是一个二元组和它们变成外部乘积二元组并单数作用于整数时产生的矩阵类型的表格。在同一行中列出的二元组将产生相同的矩阵。还有我还没有包括像表二人组合&，|，%，w，ẇ和ḍ也产生整数矩阵但他们的模式是不一样简单和很可能是更少的情况下非常有用。在线尝试wþ！

+ ------------------------------------------------- ---- +
| Dyad | 结果矩阵| 例子
+ ------------------------------------------------- ---- +
| =⁼| | 1 0 0 |
| ċ| 单位矩阵| 0 1 0 |
| | | 0 0 1 |
+ ------------------------------------------------- ---- +
| | 对角线上方的元素为1，| 0 1 1 |
| <| 其他所有元素均为0 | 0 0 1 |
| | | 0 0 0 |
+ ------------------------------------------------- ---- +
| | 对角线以下的元素为1，| 0 0 0 |
| > | 其他所有元素均为0 | 1 0 0 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| | 对角元素为0，|。0 1 1 |
| n⁻| 对角线元素为1 | 1 0 1 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| ȧ| | 1 1 1 |
| ị| 每个元素的行索引 2 2 2 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +
| oḷ| | 1 2 3 |
| ȯ| 每个元素的列索引| 1 2 3 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | 主对角线为0，上限| 0 1 2 |
| _ | 对角线是1、2 ...，较低| -1 0 1 |
| | 对角线是-1，-2 ... | -2 -1 0 |
+ ------------------------------------------------- ---- +
| | 主对角线为0，较低| 0 -1 -2 |
| _ @ | 对角线是1、2 ...，上| 1 0 -1 |
| | 对角线是-1，-2 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | 主对角线为0，上限| 0 1 2 |
| ạ| 下对角线是1，| 1 0 1 |
| | 2，3 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | | 2 3 4 |
| + | 行索引加列索引| 3 4 5 |
| | | 4 5 6 |
+ ------------------------------------------------- ---- +
| | 最少排| 1 1 1 |
| «| 和列索引| 1 2 2 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | 最大行数| 1 2 3 |
| »| 和列索引| 2 2 3 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +

列出命令和文字

如果您尝试使用许多的非矢量化list命令对文字 n或文字的列表 z，列表命令将首先转换为某种形式的名单，然后进行该名单上的命令。

这些命令iterable在jelly.py中使用该函数的调用出现。

def iterable(argument, make_copy = False, make_digits = False, make_range = False):
    the_type = type(argument)
    if the_type == list:
        return copy.deepcopy(argument) if make_copy else argument
    if the_type != str and make_digits:
        return to_base(argument, 10)
    if the_type != str and make_range:
        return list(range(1, int(argument) + 1))
    return [argument]

以下是这些列表命令将执行的操作的一些不完整列表。

包装在列表中

最简单的return from iterable将参数包装在列表中，然后返回要由函数处理的参数。如果参数还不是列表，而是字符串，并且iterable的参数不要求其他方法，则会发生这种情况。

-------------------------------------------------------------------------------
| Command | Description     | Process                       | Effect          |
-------------------------------------------------------------------------------
| F       | Flattens a list | 4953F -> [4953]F -> [4953]    | Same as W       |
-------------------------------------------------------------------------------
| G       | Format a list   | 4953G -> [4953]G -> [4953]    | Same as W       |
|         | as a grid       |                               |                 |
-------------------------------------------------------------------------------
| I       | Increments      | 4953I -> [4953]I -> <nothing> | Empty list      |
-------------------------------------------------------------------------------
| S       | Sums a list     | 4953S -> [4953]S -> 4953      | Same as ¹       |
-------------------------------------------------------------------------------
| Ṭ       | Boolean array,  | 4Ṭ -> [4]Ṭ -> [0, 0, 0, 1]    | n-1 zeroes,     |
|         | 1s at indices   |                               | 1 at end        |
-------------------------------------------------------------------------------
| Ụ       | Sort indices by | 4Ụ -> [4]Ụ -> [1]             | Yields [1]      |
|         | by their values |                               |                 |
-------------------------------------------------------------------------------
| Ė       | Enumerate list  | 4Ė -> [4]Ė -> [[1, 4]]        | Yields [[1, n]] |
-------------------------------------------------------------------------------
| Ġ       | Group indices   | 4Ġ -> [4]Ġ -> [[1]]           | Yields [[1]]    |
|         | by values       |                               |                 |
-------------------------------------------------------------------------------
| Œr      | Run-length      | 4Œr -> [4]Œr -> [[4, 1]]      | Yields [[n, 1]] |
|         | encode a list   |                               |                 |
-------------------------------------------------------------------------------

转换为基数10

此处的函数调用iterable将转换为数字D，然后转换为数字列表，然后在这些数字上运行。

-------------------------------------------------------------------------
| Command | Description     | Process                      | Effect     |
-------------------------------------------------------------------------
| Q       | Unique elements | 299Q -> [2, 9, 9]Q -> [2, 9] | Unique     |
|         | ordered by      |                              | digits     |
|         | appearance      |                              | of n       |
-------------------------------------------------------------------------
| Ṛ       | Non-vectorized  | 4953Ṣ -> [4, 9, 5, 3]Ṛ       | Reverses D |
|         | reverse         | -> [3, 5, 4, 9]              |            |
-------------------------------------------------------------------------
| Ṣ       | Sort a list     | 4953Ṣ -> [4, 9, 5, 3]Ṣ       | Sorts D    |
|         |                 | -> [3, 4, 5, 9]              |            |
-------------------------------------------------------------------------

转换为带范围的列表

此处的函数将数字转换为range R = [1 ... n]，然后在该范围内运行。

-----------------------------------------------------------------------------------------
| Command | Description       | Process                             | Effect            |
-----------------------------------------------------------------------------------------
| X       | Random element    | 4R -> [1 ... 4]X -> 2               | Random element    |
|         |                   |                                     |  of R             |
|         |                   |                                     |                   |
-----------------------------------------------------------------------------------------
| Ḋ       | Dequeue from list | 4R -> [1 ... 4]Ḋ -> [2, 3, 4]       | Range [2 ... n]   |
-----------------------------------------------------------------------------------------
| Ṗ       | Pop from list     | 4Ṗ -> [1 ... 4]Ṗ -> [1, 2, 3]       | Range [1 ... n-1] |
-----------------------------------------------------------------------------------------
| Ẇ       | Sublists of list  | 4Ẇ -> [1 ... 4]Ẇ                    | All sublists of R |
|         |                   | -> [[1], [2], [3], [4], [1, 2],     |                   |
|         |                   |     [2, 3], [3, 4], [1, 2, 3],      |                   |
|         |                   |     [2, 3, 4], [1, 2, 3, 4]]        |                   |
-----------------------------------------------------------------------------------------
| Ẋ       | Shuffle list      | 4Ẋ -> [1 ... 4]Ẋ -> [2, 1, 3, 4]    | Shuffles R        |
-----------------------------------------------------------------------------------------
| Œ!      | All permutations  | 3Œ! -> [1, 2, 3]Œ!                  | All permutations  |
|         | of a list         | -> [[1, 2, 3], [1, 3, 2],           | of R              |
|         |                   |     [2, 1, 3], [2, 3, 1],           |                   |
|         |                   |     [3, 1, 2], [3, 2, 1]]           |                   |
-----------------------------------------------------------------------------------------
| ŒḄ      | Non-vectorized    | 4ŒḄ -> [1 ... 4]ŒḄ                  | Bounces R         |
|         | bounce,           | -> [1, 2, 3, 4, 3, 2, 1]            |                   |
|         | z[:-1] + z[::-1]  |                                     |                   |
-----------------------------------------------------------------------------------------
| Œc      | Unordered pairs   | 4Œc -> [1 ... 4]Œc                  | Unordered pairs   |
|         | of a list         | -> [[1, 2], [1, 3], [1, 4], [2, 3], | of R              |
|         |                   |     [2, 4], [3, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| Œċ      | Unordered pairs   | 4Œċ -> [1 ... 4]Œċ                  | Unordered pairs   |
|         | with replacement  | -> [[1, 1], [1, 2], [1, 3], [1, 4], | with replacement  |
|         | of a list         |     [2, 2], [2, 3], [2, 4], [3, 3], | of R              |
|         |                   |     [3, 4], [4, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| ŒP      | Powerset of       | 3ŒP -> [1 ... 3]                    | Powerset of R     |
|         | a list            | -> ['', [1], [2], [3], [1, 2],      |                   |
|         |                   |     [1, 3], [2, 3], [1, 2, 3]]      |                   |
-----------------------------------------------------------------------------------------
| Œp      | Cartesian         | 4,2Œp -> [[1 ... 4], [1 ... 2]]Œp   | Cartesian product |
|         | product of z's    | -> [[1, 1], [1, 2], [2, 1], [2, 2], | of [1 ... z[i]]   |
|         | items             |     [3, 1], [3, 2], [4, 1], [4, 2]] | for i in z        |
-----------------------------------------------------------------------------------------

当正好有两个输入时，有时值得从标准输入中读取

Jelly经过优化，可以从命令行参数中获取输入。但是，它也针对编写单子而不是双子进行了优化。对于二元组，每个内建函数都有很多可能的含义，以至于您经常需要花费字符来消除歧义，而对于二元组，通常有很多方法可以表达相同的意思。

这样，如果您仅使用一次两个输入之一，而问题是无法轻易地从中隐式读取⁴（即，您需要进行⁴显式显示，或者在}，@等上花一个字符） ，请考虑从标准输入中读取，Ɠ而不是将其放在命令行中；这样，您就可以通过放置精确地将输入正确地放置在所需的位置Ɠ，同时确保所有其他隐式输入都将从其他输入中获取。这会花费一个字节并保存一个字节，并且根据问题，通过为您提供更大的范围来重新排序代码，可以很好地节省第二个字节。

有几种使用的非显而易见的方法来检查参数的属性Ƒ。以下是一些。我遗漏了此快速键（例如AƑ，，）的大量用法ŒuƑ，3Ƒ因为它们已经是实现其行为的最直接的方法。

OƑ  Is number?
ỌƑ  Is character? (errors on negative numeric input)
ḂƑ  Between 0 and 2? 0<=x<2 (python). <2aAƑƊ or of course ⁼Ḃ$ in Jelly.
ḞƑ  Is integer?
UƑ  Like `ŒḂ`, but checks if all sublists of depth 1 are palindromes.
ṠƑ  Is one of -1, 0, 1? (e-r1¤$)

随时进行编辑以添加更多有趣的案例。

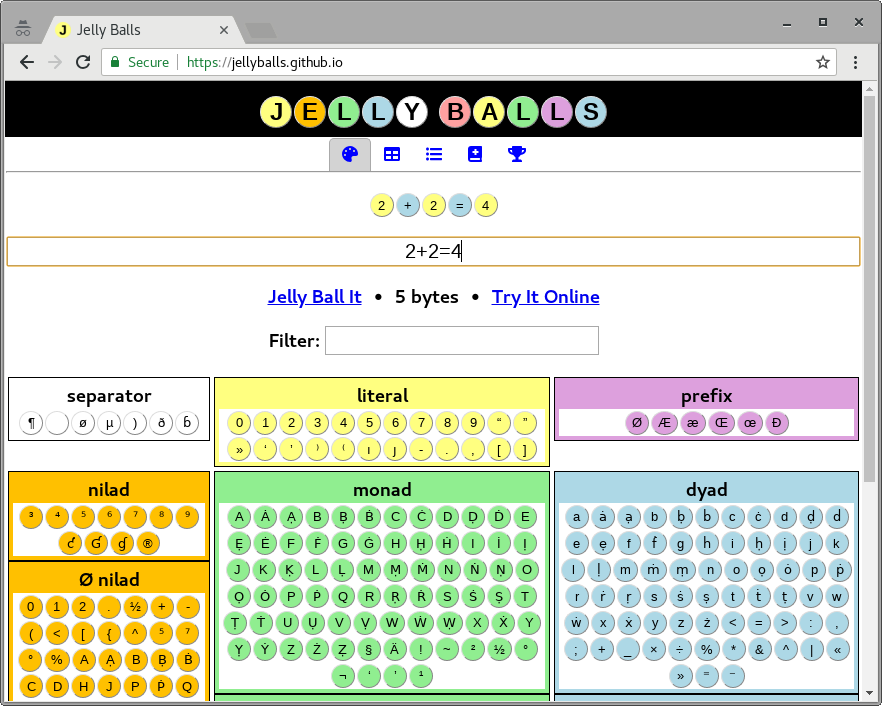
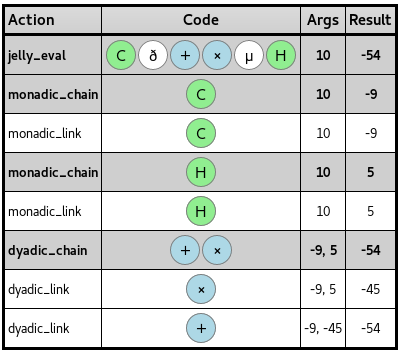
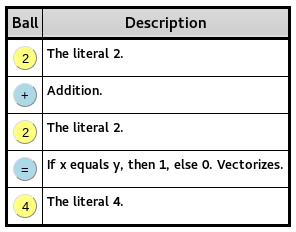
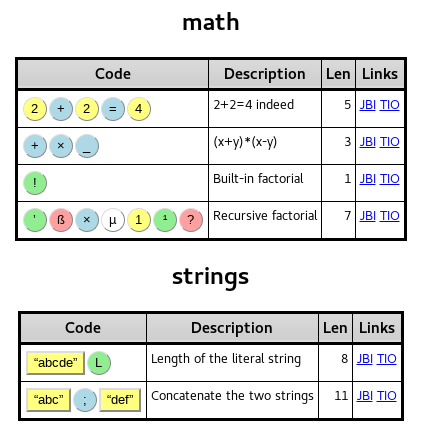
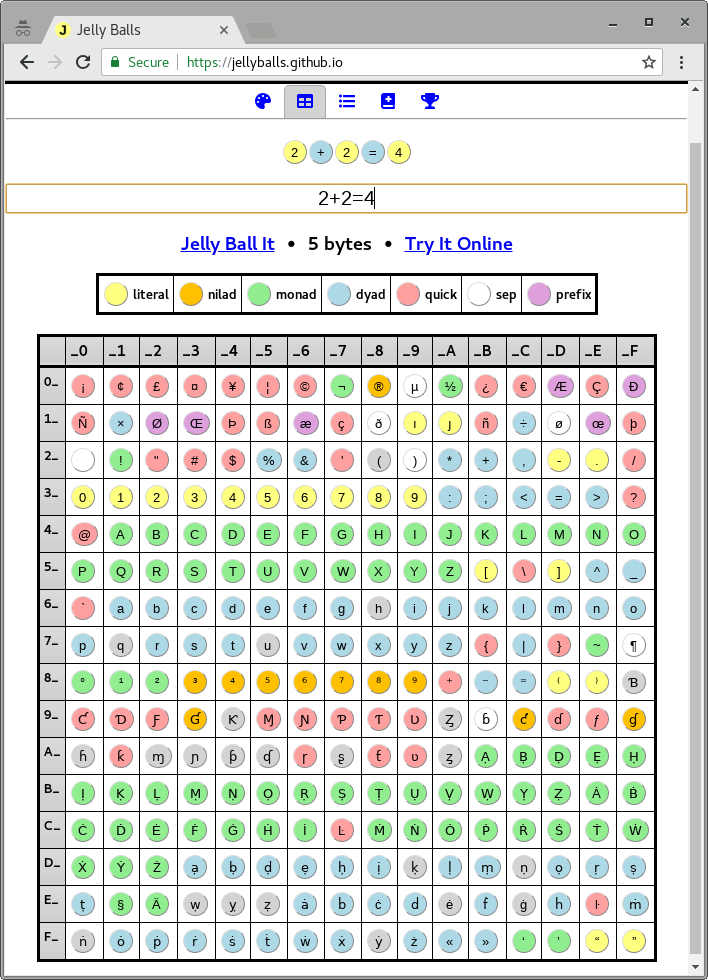
您可能需要尝试使用在线编辑器Jelly Balls来设计，以轻松地用Jelly Language构建代码。

功能包括：

• 命令面板，其中所有原子和语法字符均按类型组织
• 在线解析器识别代码中的文字和2字节原子
• 简化的浏览器内Jelly解释程序，可在javascript中的网页上运行您的Jelly代码
• 用于将代码传输到TIO或另一个Jelly Balls会话的直接链接
• 自动提示
• 针对移动设备进行了优化

尝试一下：https : //jellyballs.github.io

• 详细的跟踪报告，显示每个执行步骤的参数和结果

• 代码报告显示每个步骤的描述

• 带有果冻示例的食谱页面

• 256个Jelly字符的交互式代码页