是否可以避免合并排序中的“除法”步骤？

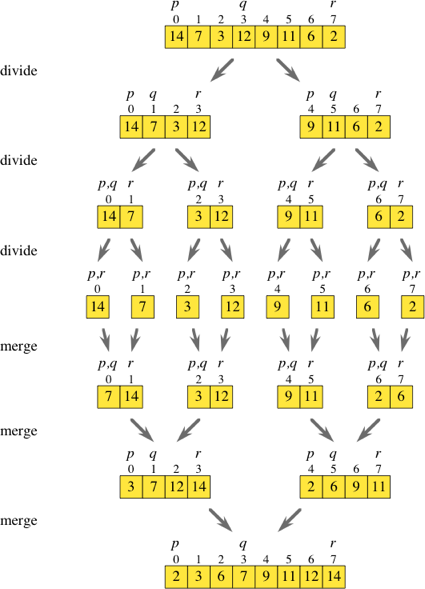
因此，合并排序是一种分而治之的算法。在查看上图时，我在考虑是否有可能基本上绕过所有划分步骤。

如果您在原始数组上跳两次时迭代原始数组，则可以在索引i和i + 1处获取元素，然后将它们放入自己的排序数组中。一旦拥有所有这些子数组（如图所示，[[7,14]，[3,12]，[9,11]和[2,6]），您就可以简单地进行常规合并例程来获取排序数组。

遍历数组并立即生成所需的子数组是否比整体执行除法步骤效率低？

混淆的产生是由于算法的概念描述与实现之间的差异。

逻辑上将合并排序描述为将数组拆分为较小的数组，然后将它们合并在一起。但是，“拆分数组”并不意味着“在内存中创建一个全新的数组”或类似的东西-它可以在代码中实现为

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

也就是说，没有实际的工作发生，“分裂”纯粹是概念上的。因此，您的建议当然可以工作，但是从逻辑上讲，您仍在“拆分”阵列-您只需要从计算机上进行任何工作即可：-)

我想你的意思是自下而上的实现。在自下而上的实现中，您将从单个单元格元素开始，通过将元素合并到更大的排序列表/数组中来向上移动。只需从中间数组（即一个元素的数组）开始反转上图中的箭头。

另外，您可能希望通过分割数组来优化合并排序，直到它们达到某个恒定大小为止，然后您可以简单地使用例如插入排序对它们进行排序。

否则，无法进行不拆分数组的排序。实际上，合并排序的要点是对子数组进行分割和排序，即分治。