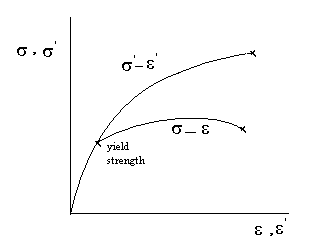为什么我们还要使用工程压力？

12

令人惊讶的是，以前没有人问过这个问题，所以我一定错过了一些简单的事情。

在该方程中，我们使用工程应力和工程应变。应力=（杨氏模量）×（应变）。这个等式用于分析弯曲梁，扭曲轴和屈曲。因此，弯曲的最终方程和扭转力 $(\frac{M}{I} = \frac{\sigma}{y})$ 会给我们带来工程应力的价值，但不会给我们带来应力的价值。 $(\frac{T}{I} = \frac{\tau}{r})$

为什么我们在知道工程应力不会给出正确的应力值的同时考虑工程应力而不是真实应力？

我读到的一些东西是：

难以测量。
差别不大，我们可以应用安全系数。
“我们不考虑材料在加载后会改变其横截面积，因为我们设计为没有塑性变形，所以弹性区域最为重要，因此在比例极限之后发生的情况并不重要”

首先，1和2对我而言并不是真正的原因。因为我们总是在弹性区域进行设计，所以数字3似乎是合理的，但这是吗？在比例极限之后，工程应变是否还能提供有效信息？

materials structural-engineering stresses

— 杰西卡（Jessica）
source

6

工程中的近似值比比皆是。谨慎的工程师知道这种近似的适用性和局限性。

— 保罗

12

我们使用工程应变，即使它不是“正确的”值，因为在大多数情况下，特别是在弹性状态下，工程应变与真实应变的差异可以忽略不计。

对于线性弹性的Hookean材料，通常在弹性极限处的应变很小。甚至最强钢，例如，有一个上限，当冷加工关于。钢的模量约为。因此为最强的钢。因此，在塑性变形开始时，工程应变为。许多有用的弹性材料在其弹性极限处具有低得多的工程应变。 $\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$ $E=200\times 10^{9}\ \textrm{Pa}$ $\varepsilon_{\textrm{el}}=0.005=0.5\%$ $0.5\%$

对于各向同性的Hookean弹性固体，以下成立

ε_{X_{1个}} = \frac{1个}{Ë} [σ_{X_{1个}} - ν （ σ_{X_{2}} + σ_{X_{3}} ）]

$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$

在选择不会失去一般性。所以在弹性极限单轴拉伸，假定材料可以自由收缩。因此 $x_{i}$ $\sigma_{x_{2}}=\sigma_{x_{3}}=0$ 。由于在弹性状态下钢的泊松比约为0.3，所以截面线性压缩应变为。因此在弹性极限的横截面面积是，或非常接近倍原始面积。 $\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$ $\nu$ $0.0015$ $(1-0.0015)^{2}A_{0}$ $0.997$

因此，真实应变为 $\frac{1}{0.997}$ $1.003$ $0.3\%$

尽管上述分析对于线弹性的Hookean固体是相当有用的，但对于聚合物和生物材料却不太适用。此类材料通常是粘弹性的（或完全是另一类材料），因此在其行为方面遵循不同的规则。真正的应变也相当发散从似地工程菌在塑性区，如下面的情节证据（发现这里）

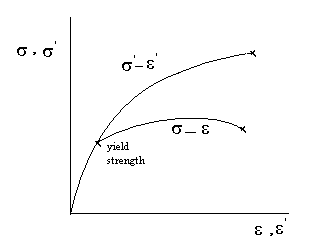
真应力真应变图

至于你的观点：

变形过程中的横截面面积的变化测量是困难的。它要求将经过校准的仪器小心地放置在经过精确加工的测试样品上。可以使用置于拉力棒侧面的应变仪来测量拉力测试设备中单轴拉伸和压缩时的横向应变。获得具有统计意义的结果需要花费大量样本，以及大量的时间，精力和成本。
$0.3\%$
我们可以忽略弹性状态结束后的任何事物，或者我们总是为弹性状态设计的想法是不正确的。塑性变形通常值得研究。要对连续的成形过程（例如轧制，拉伸，挤压等）进行建模，需要对塑性变形的机理有深入的了解，才能成功执行，为此，真实的应力和真实的应变是无价的。专门用于拉丝，请参阅（pdf）并找到方程式7。塑性变形对于在某些预期使用情况下必须永久变形的材料进行建模也很有用，例如在碰撞过程中的车身面板和车架部件。塑性变形是有用的，因为它吸收了动能。

编辑：对不起，我实际上没有回答压力这个问题。但是，应该很清楚的是，鉴于它们在弹性状态下的线性关系，这些点同样适用于应力。同样，在塑性状态下，可能会有很大的变化。

— 沃林纳
source

9

添加到@starrise的答案：

关于您撤消原因1和2的原因，您忘记了考虑有关它们的成本效益分析。正如@starrise在他们的答案中表明的那样，差异通常并不大（尽管其他材料通常会有较大差异）。

$\pm6\%$ $\pm15\%$

因此，如果所有其他特性（包括屈服强度和横截面尺寸）都将具有随机波动，而由于使用这些部件而几乎肯定会淹没“错误”，那么在日常工程实践中考虑真正应变的意义何在？工程应变而不是真实应变？

— 芥末
source