这个问题可以在O(polylog(b))中解决。
我们定义f(d, n)为不超过d个十进制数字的整数,其数字总和小于或等于n。可以看出,该函数由公式给出

让我们从更简单的内容开始派生此功能。
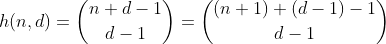
函数h计算从包含n + 1个不同元素的多集中选择d-1个元素的方式的数量。这也是将n划分为d个容器的方法的数量,可以通过在n个栅栏周围构建d-1栅栏并对每个分离的部分求和来很容易地看出。n = 2,d = 3'的示例:
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
因此,h计算具有n位和d位数字总和的所有数字。除非它仅对n小于10有效,因为数字限制为0-9。为了将其固定为值10-19,我们需要减去一个分区的分区数大于9,从现在开始,我将其称为溢出分区。
可以通过以下方式重用h来计算该项。我们计算分割n-10的方法的数量,然后选择将10放入其中的垃圾箱之一,这将导致具有一个溢出垃圾箱的分区数。结果是以下初步功能。
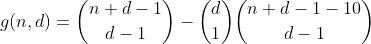
我们通过计算对n-20进行分区的所有方式,然后选择2个bin(将10放入其中),从而对n小于或等于29的方式继续进行此操作,从而计算包含2个溢出bin的分区数。
但是在这一点上,我们必须要小心,因为在上一项中我们已经计算了具有2个溢出仓的分区。不仅如此,而且实际上我们对它们进行了两次计数。让我们使用一个示例,查看总和为21的分区(10,0,11)。在上一项中,我们减去了10,计算了其余11个分区的所有分区,然后将10放入3个bin中的一个。但是可以通过以下两种方法之一来达到此特定分区:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
由于我们在第一项中也对这些分区进行了一次计数,因此具有2个溢出箱的分区的总数为1-2 = -1,因此我们需要通过添加下一项来对其进行计数。
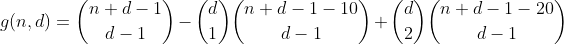
再仔细考虑一下,我们很快就会发现,可以用下表来表示在特定术语中具有特定数量的溢出垃圾箱的分区的计数次数(第i列是术语i,第j行是j溢出的分区垃圾箱)。
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
是的,它是帕斯卡三角形。我们唯一感兴趣的计数是第一行/列中的计数,即具有零溢出箱的分区数。而且由于每行的交替总和,但第一行等于0(例如1-4 + 6-4 + 1 = 0),所以我们摆脱了它们,得出倒数第二个公式。
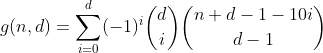
此函数计算d位数字总和为n的所有数字。
现在,数字总和小于n的数字呢?我们可以对二项式加上归纳参数使用标准递归来表明
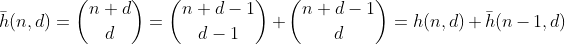
计算最多为n的数字总和的分区数。从中可以使用与g相同的参数得出f。
使用此公式,我们可以找到例如8000到8999之间的重数个数,例如 1000 - f(3, 20),因为此区间内有数千个数,并且我们必须减去数字总和小于或等于28的数个数同时考虑到第一个数字已经为数字总和贡献了8。
作为更复杂的示例,让我们看一下间隔1234..5678中的大量数字。我们首先可以以1的步长从1234到1240。然后,以10的步长从1240到1300。上面的公式为我们提供了每个这样的间隔中的重数数量:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
现在我们从1300到2000,以100为步长:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
从2000到5000,以1000为步长:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
现在我们必须再次减小步长,以100步从5000减小到5600,以10步从5600减小到5670,最后以1步从5670减小到5678。
一个示例Python实现(同时进行了一些优化和测试):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
编辑:用优化的版本替换了代码(看起来比原始代码还要难看)。还修复了一些我遇到的棘手问题。 heavy(1234, 100000000)我的机器大约需要一毫秒的时间。
