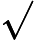P / poly中是否包含NPI？

据推测因为相反的话就意味着\ mathsf {PH} = \ Sigma_2。拉德纳定理确定，如果\ mathsf {P} \ ne \ mathsf {NP}则\ mathsf {NPI}：= \ mathsf {NP} \ setminus（\ mathsf {NPC} \ cup \ mathsf {P}）\ ne \ emptyset。但是，证明似乎并未推广到\ mathsf {P} / \ text {poly}，因此，可能性\ mathsf {NPI} \ subset \ mathsf {P} / \ text {poly}即\ mathsf {NP} \子集\ mathsf {NPC} \ cup \ mathsf {P} / \ text {poly}似乎是开放的。$\mathsf{NP} \nsubseteq \mathsf{P}/\text{poly}$$\mathsf{PH} = \Sigma_2$$\mathsf{P} \ne \mathsf{NP}$$\mathsf{NPI} := \mathsf{NP} \setminus(\mathsf{NPC} \cup \mathsf{P}) \ne \emptyset$$\mathsf{P}/\text{poly}$$\mathsf{NPI} \subset \mathsf{P}/\text{poly}$$\mathsf{NP} \subset \mathsf{NPC} \cup \mathsf{P}/\text{poly}$

假设$\mathsf{NP} \nsubseteq \mathsf{P}/\text{poly}$（甚至多项式层次结构不会在任何级别折叠），则为$\mathsf{NPI} \subset \mathsf{P}/\text{poly}$是真的还是假的？有什么证据可以支持和反对呢？

根据Schöning对Ladner定理的推广，这是填充参数的一种可能替代方案。要理解这一论点，您需要访问本文（不幸的是，对于许多人来说，这将是酬金的背后）：

UweSchöning。在复杂度类中获得对角线集合的统一方法。理论计算机科学18（1）：95-103，1982。

我们将应用该论文的主要定理，将和作为语言，并将和作为复杂度类，如下所示：$A_1$$A_2$$\mathsf{C}_1$$\mathsf{C}_2$

• $A_1 = \varnothing$（或任何语言）$\mathsf{P}$
• $A_2 = \text{SAT}$
• $\mathsf{C}_1 = \mathsf{NPC}$
• $\mathsf{C}_2 = \mathsf{NP} \cap \mathsf{P/poly}$

为了清楚起见，我们将证明的事实是意味着。$\mathsf{NP} \not\subseteq \mathsf{P/poly}$$\mathsf{NPI} \not\subseteq \mathsf{P/poly}$

在的假设下，我们有和。显然，和在有限的变化下是封闭的。Schöning的论文包括证明是递归可表示的（可以在论文中找到其确切定义），而该论证中最难的部分是证明是递归可表示的。$\mathsf{NP} \not\subseteq \mathsf{P/poly}$$A_1\not\in\mathsf{C}_1$$A_2\not\in\mathsf{C}_2$$\mathsf{C}_1$$\mathsf{C}_2$$\mathsf{C}_1$$\mathsf{C}_2$

在这些假设下，该定理暗示存在一种语言，它既不在也不在；并假设，则认为是Karp可还原为，因此。假设在但既不是也不在，则得出。$A$$\mathsf{C}_1$$\mathsf{C}_2$$A_1\in\mathsf{P}$$A$$A_2$$A\in\mathsf{NP}$$A$$\mathsf{NP}$$\mathsf{NP}$$\mathsf{NP} \cap \mathsf{P/poly}$$\mathsf{NPI} \not\subseteq \mathsf{P/poly}$

有证据证明是递归可表示的。基本上，这意味着存在对确定性图灵机的序列的明确描述，这些图灵机都在所有输入上都停止，并且使得。如果我的论点有误，可能是在这里，如果您确实需要使用此结果，则需要仔细进行操作。无论如何，通过对所有多项式时间非确定性图灵机（可以确定性地进行仿真，因为我们不在乎每个的运行时间）进行$\mathsf{NP} \cap \mathsf{P/poly}$$M_1, M_2, \ldots$$\mathsf{NP} \cap \mathsf{P/poly} = \{L(M_k):k=1,2,\ldots\}$$M_k$）以及代表给定语言的布尔电路族大小上限的所有多项式，我相信获得有效的枚举并不困难。本质上，每个可以通过搜索所有可能的布尔电路来测试其对应的多项式时间NTM是否与某些多项式大小的电路家族相符，直到输入字符串的长度为止。如果达成协议，则像NTM那样输出，否则会拒绝（因此表示一种有限的语言）。$M_k$$M_k$

该参数背后的基本直觉（隐藏在Schöning的结果之内）是，您永远不能使两个“不错的”复杂性类（即具有递归表示的类）不相交并且彼此齐平。复杂类的“拓扑”是不允许的：您可以始终在两个类之间适当地构造语言，方法是以某种方式在两个类之间交替使用以获得极长的输入长度。Ladner定理针对和展示了这一点，而Schöning的概括使您可以对许多其他类进行相同的处理。$\mathsf{P}$$\mathsf{NPC}$

我只想写下注释中描述的某个版本的padding参数。我不明白为什么需要差距。我们想证明如果P / poly中不包含NP，则存在P / poly中不包含NP中间问题。

有一个无界函数，使得SAT的电路大小不小于，因此有一个函数是无界的，递增的，并且。让SAT”表示由填充长度的SAT串获得的语言至。然后：$f$$n^{f(n)}$$g$$g(n)=o(f(n))$$n$$n^{g(n)}$

• SAT'在NP中（请参阅下文！）
• SAT'不在P / poly中：给定SAT'的电路尺寸为，我们得到SAT的电路尺寸为，但小于对于一些。$n^k$$n^{g(n)k}$$n^{f(n)}$$n$
• 从SAT到SAT'没有P / poly减少：假设矛盾是，有SAT 大小为电路，允许SAT'门。挑足够大，使得和让。每个SAT'门最多具有输入。通过删除填充输入，我们可以将的SAT'门修剪为少于输入的SAT门，我们可以使用进行模拟-最终的SAT'门最多输入。重复此过程并用手处理，SAT的电路大小约为$C_n$$n^k$$N$$g(\sqrt{N}) > 2k$$n>N$$C_n$$n^k$$C_n$$\sqrt{n}$$C_{\sqrt{n}}$$n^{k/2}$$C_N$$O(n^k n^{k/2} n^{k/4} \dots) \approx O(n^{2k})$对于某些小于。$n^{f(n)}$$n$

编辑：

的选择有些麻烦。如果您乐意将SAT'放入NP的承诺版本中，则不需要此位。$g$

将定义为最大整数，以使SAT的长度为字符串不存在大小为电路。通过一种算法定义，该算法计算，在时间或之后停止并返回，并返回此时找到的最大值的平方根的下限。因此是无界的，并且和可以在时间计算出来。现在请注意，对于无限多的，上述论点仅依赖于没有大小为电路的SAT$f(n)$$n^{f(n)}$$n$$g(n)$$f(m)$$m=1,2,\dots$$n$$m=n$$g(n)$$\liminf g(n)/f(n)=0$$g(n)$$n$$n^{f(n)}$$n$。

我也觉得很有趣，例如http://blog.computationalcomplexity.org/media/ladner.pdf中的SAT漏洞证明。没有NP要求，这是相当容易的：存在一个序列，使得没有电路os size可以检测到长度为 SAT字符串；对于某些将SAT限制为长度为字符串。$n_1<n_2<\dots$$(n_k)^k$$n$$n_{2^{2^i}}$$i$

（NPI P / poly）（P NP）$\nsubseteq$$\implies$$\neq$