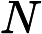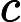我们是否应将

许多专家认为猜想是正确的，并将其用于结果中。我担心的是，复杂度很大程度上取决于P ≠ N P猜想。$\mathsf{P} \neq \mathsf{NP}$$\mathsf{P} \neq \mathsf{NP}$

所以我的问题是：

只要没有证明猜想，就可以/应该将其视为自然定律吗？还是应该将其视为 可能在某一天被证明或被证明不正确的数学猜想？$\mathsf{P}\neq\mathsf{NP}$

引用：

“支持库克和瓦利安特假设的证据如此之多，而且它们失败的后果是如此怪诞，以至于它们的地位也许可以与物理定律相比，而不是普通的数学猜想。”

[ 1986年，沃克·斯特拉森（Volker Strassen）对Nevanlinna奖获得者Leslie G. Valian 的称赞 ]

在阅读TCS中的物理结果后，我会问这个问题吗？。可能有趣的是注意到计算复杂度与（理论）物理有一些相似之处：许多重要的复杂度结果通过假设来证明，而在理论上，物理结果通过假设某些物理定律来证明$\mathsf{P} \neq \mathsf{NP}$。从这个意义上讲，可以将视为E = m c 2。回到TCS的物理结果？：$\mathsf{P} \neq \mathsf{NP}$$E = mc^2$

TCS（的一部分）可以成为自然科学的分支吗？

澄清：

（请参阅下面的Suresh的回答）

可以说，复杂性理论中的猜想与理论物理学中的物理定律一样基本（如Strassen所说）吗？$\mathsf{P}\neq\mathsf{NP}$

Strassen的声明需要放在上下文中。1986年，这是对数学家的演讲，当时许多数学家对理论计算机科学没有很高的评价。完整的陈述是

对于某些人来说，这里讨论的理论似乎建立在薄弱的基础上。他们不。支持库克和瓦朗特假说的证据是如此压倒性的，而且它们失败的后果是如此怪诞，以至于它们的地位也许可以与物理定律相比，而不是普通的数学猜想。

我确定斯特拉森已经与纯粹的数学家进行过对话，他们按照

“您将整个复杂性理论建立在纸牌屋的基础上。如果P = NP怎么办？那么您的所有定理都将毫无意义。为什么您不花一点力气就证明P NP，而不是继续在如此薄弱的基础上建立理论。”$\neq$

在2013年，当P NP成为克莱奖问题十二年时，似乎很难相信任何数学家实际上都持这种态度。但是，我可以亲自证明其中一些做法。$\neq$

Strassen继续说，我们不应该放弃寻找P NP 的证明（因此间接暗示这确实是数学上的猜想）：$\neq$

尽管如此，传统的证明还是很有意思的，在我看来，瓦利恩特的假设可能比库克的假设更容易确认。

所以也许我将其标记为“有效假设”，而不是“物理定律”。

最后让我指出，数学家也使用这样的假设。有大量证明定理的数学论文的陈述为“假设黎曼假设成立，然后……”。

我可以看到三种相关的方式来理解这个问题：

1）甚至在我们不能证明它之前，我们是否可以将视为计算复杂性理论的基本原理？$NP \ne P$

2）原理是否超出了其狭义的数学意义？$NP \ne P$

3）原理是否可以视为物理定律？$NP \ne P$

我认为对于这三个问题，都有充分的理由回答“是”或“合格的是”。

我不确定我是否理解。物理定律（您所指示的那种）是声称捕获现实的模型的数学表达式（在该示例中为相对论）。如果基础数学不正确，则可以证明物理定律是错误的，但是如果基础模型发生变化，则物理定律也可能是错误的（例如，牛顿力学）。P vs NP是一个特殊的数学猜想，是对还是错（可能是可证明的）

要回答您的原始问题：

$P \ne NP$

“ NP硬度假设？：没有物理方法可以在多项式时间内解决NP完全问题”。

他在滑铁卢大学作了题为“ 计算难易度为物理定律”的精彩演讲。

$NL\neq PSPACE$$NP\neq coNP$$P\neq NP$

$\phi$$\phi$

您可以对速度和速度进行大量实验，并且将获得压倒性的证据来验证牛顿定律。当然，在非常特殊的实验中，您会看到一些非常奇怪的东西，例如流动水中的光速或一些天文事件。但是，您的绝大多数证据都会对您说：牛顿是对的，而这些法律正是您所需要的

当然，牛顿“是不对的”，爱因斯坦紧随其后。

对于P = NP，我们可以看到很多例子，其中P≠NP。但是在某些特定情况下，我们有奇怪的事情。如果P≠NP，则它们之间存在无数类，因此我们应该在NP中发现一些不在P中但不完整的问题。我们不认识他们，大多数候选人都被证明是P。

您对这个问题的看法取决于您要看的地方。如果P = NP，我不会感到惊讶。