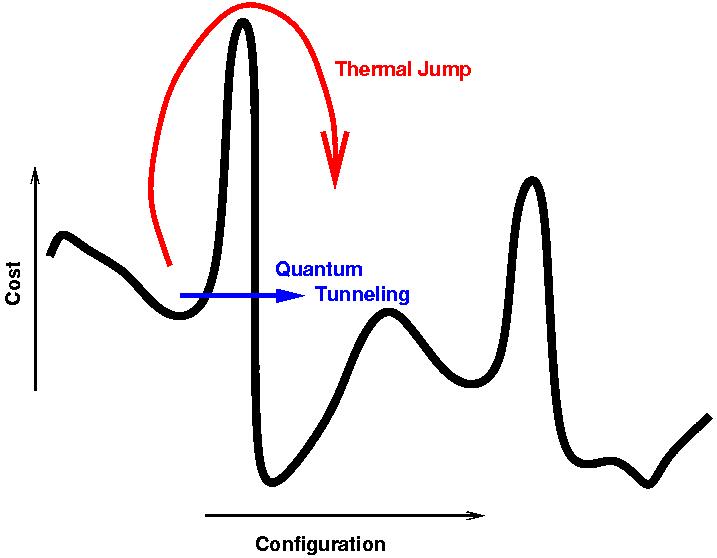
为什么不能用门模型描述量子退火？

基于这个问题，我被启发提出了一个问题，该问题指出，量子退火与通常的电路模型是完全不同的计算模型。我以前已经听说过，并且据我了解，门模型不适用于量子退火，但是我从未完全理解为什么这样做，或者如何解析退火器可以进行的计算。据我从几次谈话中了解到的（退火炉本身就是D波！），退火炉仅限于特定的哈密顿量。

的量子退火炉，如d波机是伊辛模型的物理表示，因此具有“问题”的形式的哈密顿

本质上，要解决的问题映射到上述哈密顿量。该系统开始与哈密顿和退火参数，š用于将初始哈密顿映射ħ 我到该问题哈米尔顿算ħ P使用ħ （小号） = （1 - 小号）ħ 我 + 小号ħ P。$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

由于这是退火，因此该过程进行得足够缓慢，以保持在系统的基态附近，而哈密顿量随问题而变化，使用隧道方法保持在基态附近，如Nat的答案所述。

现在，为什么不能用它来描述门模型质量控制？上面是一个NP难的二次无约束二进制优化（QUBO）问题。实际上，这是一篇将许多NP问题映射到Ising模型的文章。NP中的任何问题都可以映射为多项式时间内的任何NP难题，而整数分解确实是NP问题。

嗯，温度不为零，因此在整个退火过程中不会处于基态，因此，解决方案仍然只是一个近似值。或者，换句话说，失败的概率大于一半（与通用QC认为“不错”的成功概率相差无几）-根据我所看到的图表判断，成功的概率为当前的机器大约为并且只会随着大小的增加而变得更糟），并且退火算法不是有界误差。完全没有 因此，无法通过整数分解等方法来了解您是否具有正确的解决方案。$0.2\%$

它（原则上）所做的是非常快地非常接近精确结果，但这对于需要精确结果的任何事情都无济于事，因为从“几乎正确”到“正确”的转换仍然非常困难（也就是说，在这种情况下，当原始问题出在NP问题上时，一般来说大概还是NP），因为/提供“近乎正确”的解决方案的参数不一定会分布在/给出的参数附近。正确的解决方案。

编辑以澄清问题：这意味着量子退火器（QA）仍需要花费指数时间（尽管可能需要更快的指数时间）来解决诸如整数分解之类的NP问题，其中通用QC可以加快指数速度并解决相同的问题。聚时间问题。这就是说，质量保证不能在多边形时间内模拟通用质量控制（否则它可以解决在多边形时间内无法解决的问题）。正如在评论中指出，这并不等于说，一个QA不能给予同样的加速在其他的问题，比如数据库搜索。

退火更像是一种模拟策略。

要点是您有一些要优化的怪异功能。因此，您在它周围反弹。首先，“ 温度 ”很高，因此所选点可能会反弹很多。然后，随着算法“ 冷却 ”，温度下降，弹跳变得不那么积极。

最终，它会稳定到局部最优值，理想情况下，局部最优值就像全局最优值一样。

这是用于模拟退火（非量子）的动画：

但是，量子退火的概念几乎相同：

相比之下，门逻辑比数字逻辑要多得多。它关注的是量子位和逻辑运算，而不仅仅是在混乱的反弹之后找到结果。